Gaussian Processes
Gaussian process $f$ — random function with jointly Gaussian marginals.
Characterized by
- a mean function $m(x) = \E(f(x))$,
- a kernel (covariance) function $k(x, x') = \Cov(f(x), f(x'))$.
Notation: $f \~ \f{GP}(m, k)$.
The kernel $k$ must be positive (semi-)definite (non-trivial requirement).
Gaussian Process Regression
Takes
- data $(x_1, y_1), .., (x_n, y_n) \in X \x \R$,
- and a prior Gaussian Process $\f{GP}(m, k)$
giving the posterior (conditional) Gaussian process $\f{GP}(\hat{m}, \hat{k})$.
The functions $\hat{m}$ and $\hat{k}$ may be explicitly expressed in terms of $m$ and $k$.
Standard Priors
Matérn Gaussian Processes
$$
\htmlData{class=fragment fade-out,fragment-index=6}{
\footnotesize
\mathclap{
k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\abs{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\abs{x-x'}}{\kappa}}
}
}
\htmlData{class=fragment d-print-none,fragment-index=6}{
\footnotesize
\mathclap{
k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\abs{x-x'}^2}{2\kappa^2}}
}
}
$$
$\sigma^2$: variance
$\kappa$: length scale
$\nu$: smoothness
$\nu\to\infty$: RBF kernel (Gaussian, Heat, Diffusion)
$\nu = 1/2$
$\nu = 3/2$
$\nu = 5/2$
$\nu = \infty$
This talk: "Nice" priors on non-Euclidean domains
Be able to: evaluate $k(x, x')$, differentiate it, sample $\mathrm{GP}(0, k)$.
Non-Euclidean Domains

Manifolds
e.g. in physics (robotics)
Graphs
e.g. for road networks
Spaces of graphs
e.g. for drug design
Distance-based Approach
$$ k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2\exp\del{-\frac{|x - x'|^2}{2\kappa^2}} $$
$$ k_{\infty, \kappa, \sigma^2}^{(d)}(x,x') = \sigma^2\exp\del{-\frac{d(x,x')^2}{2\kappa^2}} $$
Manifolds: not PSD for some $\kappa$ (in some cases—for all) unless the manifold is isometric to $\mathbb{R}^d$.
Feragen et al. (CVPR 2015) and Da Costa et al. (SIMODS 2025).
Graph nodes: not PSD for some $\kappa$ unless can be isometrically embedded into a Hilbert space.
Schoenberg (Trans. Am. Math. Soc. 1938).
Not PSD on the square graph.
Not PSD on the circle manifold.
Another Approach: Stochastic Partial Differential Equations
$$ \htmlData{class=fragment,fragment-index=0}{ \underset{\t{Matérn}}{\undergroup{\del{\frac{2\nu}{\kappa^2} - \Delta}^{\frac{\nu}{2}+\frac{d}{4}} f = \c{W}}} } $$ $\Delta$: Laplacian $\c{W}$: Gaussian white noise $d$: dimension
Generalizes well
Geometry-aware: respects to symmetries of the space
Implicit: no formula for the kernel
Making It Explicit:
Compact Manifolds
Examples: $\bb{S}_d$, $\bb{T}^d$
Solution for Compact Riemannian Manifolds
The solution is a Gaussian process with kernel $$ \htmlData{fragment-index=2,class=fragment}{ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^\infty \Phi_{\nu, \kappa}(\lambda_n) f_n(x) f_n(x') } $$
$\lambda_n, f_n$: eigenvalues and eigenfunctions of the Laplace–Beltrami operator
$$ \htmlData{fragment-index=4,class=fragment}{ \Phi_{\nu, \kappa}(\lambda) = \begin{cases} \htmlData{fragment-index=5,class=fragment}{ \del{\frac{2\nu}{\kappa^2} - \lambda}^{-\nu-\frac{d}{2}} } & \htmlData{fragment-index=5,class=fragment}{ \nu < \infty \text{ --- Matérn} } \\ \htmlData{fragment-index=6,class=fragment}{ e^{-\frac{\kappa^2}{2} \lambda} } & \htmlData{fragment-index=6,class=fragment}{ \nu = \infty \text{ --- Heat (RBF)} } \end{cases} } $$How to get $\lambda_n, f_n$?
How to get $\lambda_n, f_n$?
Discretize the Problem
— works for general manifolds of very low dimension,
— see «Matérn Gaussian processes on Riemannian manifolds», NeurIPS 2020.
Use Algebraic Structure
— works for homogenous spaces (e.g. $\mathbb{S}_d$ or $\mathrm{SO}(n)$) of higher dimension,
— see «Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces I», (JMLR 2024) .
Examples: The Values of $k_{1/2}(\htmlStyle{color:rgb(255, 19, 0)!important}{\bullet},\.)$ on Compact Riemannian Manifolds
Circle
(Lie group)

Sphere
(homogeneous space)

Dragon
(general manifold)
Examples: Samples from $\mathrm{GP}(0, k_{\infty})$ on Compact Homgeneous Spaces
 Sphere $\mathbb{S}_2$
Sphere $\mathbb{S}_2$
 Torus $\mathbb{T}^2 = \bb{S}_1 \x \bb{S}_1$
Torus $\mathbb{T}^2 = \bb{S}_1 \x \bb{S}_1$
 Projective plane $\mathrm{RP}^2$
Projective plane $\mathrm{RP}^2$
Driven by generalized random phase Fourier features (GRPFF).
Alternative Generalization
Alternative Generalization of the RBF Kernel
Let $\mathcal{P}$ denote the heat kernel, the fundamental solution of $ \frac{\partial u}{\partial t} = \Delta_x u . $
Then, on $\mathbb{R}^d$: $$ \begin{aligned} \htmlData{fragment-index=3,class=fragment}{ k_{\infty, \kappa, \sigma^2}(x, x') } & \htmlData{fragment-index=3,class=fragment}{ \propto \mathcal{P}(\kappa^2/2, x, x'), } \\ \htmlData{fragment-index=4,class=fragment}{ k_{\nu, \kappa, \sigma^2}(x, x') } & \htmlData{fragment-index=4,class=fragment}{ \propto \sigma^2 \int_{0}^{\infty} t^{\nu-1+d/2}e^{-\frac{2 \nu}{\kappa^2} t} \mathcal{P}(t, x, x') \mathrm{d} t } \end{aligned} $$
Alternative generalization: use the above as the definition.
☺ Always positive semi-definite + Interpretable inductive bias.
☺ Usually equivalent to SPDE-based with no SPDE machinery.
☹ Implicit, requires solving the equation.
Making It Explicit:
Non-compact Manifolds
Examples: $\bb{H}_d$, $\mathrm{SPD}(d)$
The Basic Idea
For symmetric spaces like $\bb{H}_d$, $\mathrm{SPD}(d)$ harmonic analysis generalizes well.
This allows to generalize random Fourier features to this setting.
— a few technical challenges arise though.
— see «Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces II», (JMLR 2024).
Examples: The Values of $k_{\infty}(\htmlStyle{color:rgb(0, 0, 0)!important}{\bullet},\.)$ on Non-compact Manifolds
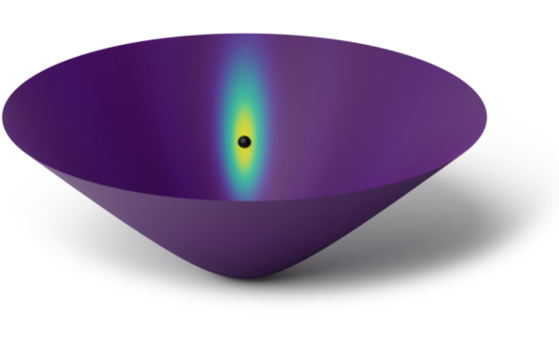 Hyperbolic space $\bb{H}_2$
Hyperbolic space $\bb{H}_2$


Space of positive definite matrices $\f{SPD}(2)$
Examples: Samples from $\mathrm{GP}(0, k_{\infty})$ on Non-compact Homgeneous Spaces
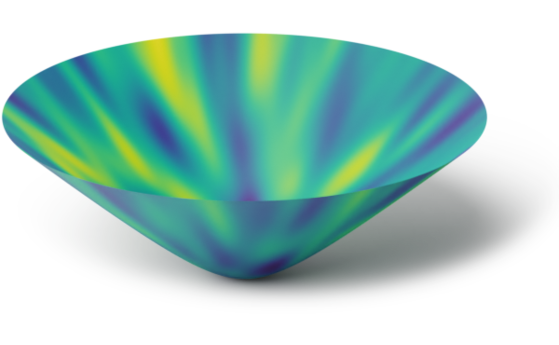 Hyperbolic space $\bb{H}_2$
Hyperbolic space $\bb{H}_2$

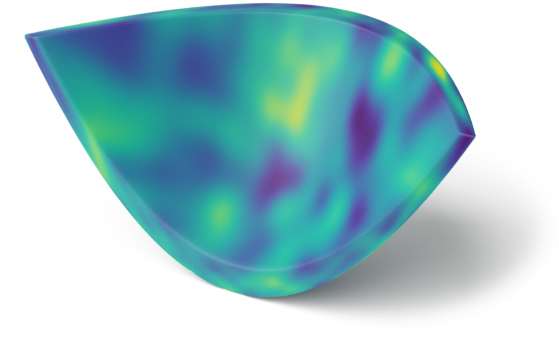
Space of positive definite matrices $\f{SPD}(2)$
Example Application
Application: Wind Speed Modeling (Vector Fields on Manifolds)

Geometry-aware vs Euclidean
Making It Explicit:
Node Sets of Graphs
Matérn Kernels on Weighted Undirected Graphs
SPDE turns into a stochastic linear system. The solution has kernel $$ \htmlData{fragment-index=2,class=fragment}{ k_{\nu, \kappa, \sigma^2}(i, j) = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^{\abs{V}-1} \Phi_{\nu, \kappa}(\lambda_n) \mathbf{f_n}(i)\mathbf{f_n}(j) } $$
$\lambda_n, \mathbf{f_n}$: eigenvalues and eigenvectors of the Laplacian matrix
$$ \htmlData{fragment-index=4,class=fragment}{ \Phi_{\nu, \kappa}(\lambda) = \begin{cases} \htmlData{fragment-index=5,class=fragment}{ \del{\frac{2\nu}{\kappa^2} - \lambda}^{-\nu} } & \htmlData{fragment-index=5,class=fragment}{ \nu < \infty \text{ --- Matérn} } \\ \htmlData{fragment-index=6,class=fragment}{ e^{-\frac{\kappa^2}{2} \lambda} } & \htmlData{fragment-index=6,class=fragment}{ \nu = \infty \text{ --- Heat (RBF)} } \end{cases} } $$Example Application
Making It Explicit:
Spaces of Graphs
Spaces of Graphs
Consider the set of all unweighted graphs with $n$ nodes.
It is finite!
How to give it a geometric structure?
Make it into a space?
Graphs define geometry of discrete sets. We make it into a node set of a graph!
Space of graphs with $n = 3$ nodes
as the $3$-dimensional cube
Spaces of Graphs
Beyond functions of actual graphs $f\big(\smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg2.svg}}\big)$, it is useful to consider functions of equivalence classes of graphs: $f\big(\big\{\smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg2.svg}}, \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg3.svg}}, \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg4.svg}}\big\}\big)$.
Space of equivalence classes for $n=4$
as the quotient graph of the $4$-d cube
Spaces of Graphs
Space of graphs with $n = 3$ nodes
as the $3$-dimensional cube
Space of equivalence classes for $n=4$
as the quotient graph of the $4$-d cube
Spaces of Graphs
Space of graphs with $n = 3$ nodes
as the $3$-dimensional cube
Space of equivalence classes for $n=4$
as the quotient graph of the $4$-d cube
Conclusion
Gaussian processes:
various geometric settings
Gaussian processes:
various geometric settings

Simple manifolds:
meshes, spheres, tori
Borovitskiy et al. (AISTATS 2020)

Compact Lie groups and
homogeneous spaces:
$\small\f{SO}(n)$, resp. $\small\f{Gr}(n, r)$
Azangulov et al. (JMLR 2024)
Non-compact symmetric
spaces: $\small\bb{H}_n$ and $\small\f{SPD}(n)$
Azangulov et al. (JMLR 2024)
Gaussian processes: various geometric settings

Vector fields on simple manifolds
Robert-Nicoud et al. (AISTATS 2024)
Gaussian processes: various geometric settings
Edges of graphs
Yang et al. (AISTATS 2024)
Metric graphs
Bolin et al. (Bernoulli 2024)
Cellular Complexes
Alain et al. (ICML 2024)
Spaces of Graphs
Borovitskiy et al. (AISTATS 2023)
Implicit geometry
Semi-supervised learning:
scalar functions
Fichera et al. (NeurIPS 2023)

Semi-supervised learning:
vector fields
Peach et al. (ICLR 2024)
Implementation
https://geometric-kernels.github.io/
Together with

Alexander
Terenin

Peter
Mostowsky

Iskander
Azangulov

Andrei
Smolensky

Mohammad Reza
Karimi

Vignesh Ram
Somnath

Noémie
Jaquier

Michael
Hutchinson

So
Takao
