ProbAI 2025
Geometric Probabilistic Models
Viacheslav (Slava) Borovitskiy
https://vab.im
Before we start:
— Largely based on the UAI 2024 Tutorial with the same name.
— The 2024 tutorial was co-created with Prof. Alexander Terenin (Cornell).
Resources: https://vab.im/probai2025/
Part I: background, motivation, technical fundamentals
- Model-based decision-making
- Probabilistic modeling and uncertainty
- Digression: Gaussian processes, the "gold standard"
- Geometric learning: working with structured data
Part II: geometric probabilistic models
- Example problem: Setup
- Basic types of probabilistic models
- Example problem: Evaluation
- Emerging applications
- Software
- Summary
References
Model-based decision-making
Model-based decision-making
: Bayesian optimization
Automatic explore-exploit tradeoff
Principle of Separation:
modeling and decision-making
Probabilistic models
Probabilistic models
Predictions and uncertainty
Uncertainty behavior
Neural network baseline
Uncertainty behavior: Practice
Deep ensembles:
- Train $K$ neural networks $f_1, \ldots, f_K$ with different initializations.
- Prediction: average $f(x) = \frac{1}{K} \sum_{k=1}^K f_k(x)$.
- Uncertainty: std deviation $\sigma(x) = (\frac{1}{K} \sum_{k=1}^K (f_k(x) - f(x))^2)^{1/2}$.
Open Notebook 1 [Google Colab]
at https://vab.im/probai2025/.
Plot the uncertainty of the ensemble.
Uncertainty behavior
Neural network ensemble
Uncertainty behavior
Bayesian neural network using MCMC
Uncertainty behavior
Gaussian process: RBF kernel
Uncertainty behavior
Gaussian process: polynomial kernel
Uncertainty behavior
Gaussian process: RBF kernel
Gaussian process: polynomial kernel
Ensemble
Bayesian neural network
Different models: different behavior
Goal: reasonable control of model's uncertainty behavior
Vague idea: regulate uncertainty using symmetries
Digression:
Gaussian processes
Gaussian processes
(GPs)
"Gold standard" for learning with uncertainty in low dimension.
Formally, GPs — random functions with jointly Gaussian marginals.
Bayesian learning: prior GP + data = posterior GP
Prior GPs are determined by kernels (covariance functions)
— have to be positive semi-definite,
— not all kernels define "good" GPs.
Standard GP priors
RBF kernel (Gaussian, Heat, Diffusion), part of a wider Matérn kernel family: $$ k_{\kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\norm{x-x'}^2}{2\kappa^2}} $$
Why is it standard?
Intuitively, the simplest possible kernel which is:
- stationary: $k(x + s, x' + s) = k(x, x')$;
- smooth: $k$ is infinitely differentiable.
Geometric learning
What are we trying to do?
Regression and classification: $$ \htmlClass{fragment}{ \min_{f\in\c{F}} \sum_{i=1}^N L(y_i, f(x_i)) } $$ where
- $(x_i,y_i)$: training data
- $L$: loss function, such as square loss $\norm{y_i - f(x_i)}^2$
- $\c{F}$: some set of functions $f : X \to Y$
Spaces $X$ and/or $Y$ carry geometric structure
What are we trying to do? An example: graphs
$$ f : V \to \R $$
$$ f\Big(\smash{\includegraphics[height=2.75em,width=1.5em]{figures/g1.svg}}\Big) = 2 $$
$$ f\Big(\smash{\includegraphics[height=2.75em,width=1.5em]{figures/g2.svg}}\Big) = 3 $$
$$ f\Big(\smash{\includegraphics[height=2.75em,width=1.5em]{figures/g3.svg}}\Big) = 5 $$
What are we trying to do?
Probabilistic regression and classification: $$ \htmlClass{fragment}{ y_i \~ p_{y\given f}(\.\given f(x_i)) } $$ where
- $(x_i,y_i)$: training data
- $p_{y\given f}$: likelihood, such as Gaussian $y_i \~\f{N}(f(x_i), \sigma^2)$
- Bayesian approach: place a prior $p_f$ over functions $f : X \to Y$
Spaces $X$ and/or $Y$ carry geometric structure
What are we trying to do? An example: graphs
$$ f : V \to \text{distributions over } \R $$
$$ f\Big(\smash{\includegraphics[height=2.75em,width=1.5em]{figures/g1.svg}}\Big) = \f{N}(2, 0.5^2) $$
$$ f\Big(\smash{\includegraphics[height=2.75em,width=1.5em]{figures/g2.svg}}\Big) = \f{N}(3, 0.2^2) $$
$$ f\Big(\smash{\includegraphics[height=2.75em,width=1.5em]{figures/g3.svg}}\Big) = \f{N}(5, 0.7^2) $$
Geometric learning: what can $X$ be?
Graphs
Spaces of Graphs

Meshes

Manifolds
And many more!
Key concepts: invariance and equivariance
Consider a dataset of images of circles of different locations and sizes:
Problem 1: find a circle's diameter
- Symmetries: translations
- Model $f$—invariant, i.e.
$$f(s \triangleright x) = f(x)$$
Problem 2: find a circle's center
- Symmetries: translations
- Model $f$—equivariant, i.e.
$$f(s \triangleright x) = s \triangleright f(x)$$
Challenges
Challenge: how do we represent data?
Two ways of representing points on a sphere:
- Points in $\R^3$: $(x,y,z) \in \R^3$ with $x^2 + y^2 + z^2 = 1$
- Angles: $(\theta,\phi)$ representing latitude and longitude

Different numbers: same point on sphere
Predictions should depend on our data, not on how we store it numerically
Challenge: how do we represent data?
Graphs can be represented as adjacency matrices in many ways.
Good models should be invariant to this ambiguity.
Challenge: training behavior
Original dataset
Shifted dataset
We want training to be equivariant to shifts:
Training on a shifted dataset should result in a shifted model.
True for stationary GPs, usually not true for neural networks.
Challenge: training behavior
Original dataset
"Shifted" dataset
For graphs, we want training to be equivariant to permutations that preserve the graph structure.
Symmetries: extrapolation and uncertainty
Design principle: models which respect the space's symmetries
- Symmetry-based extrapolation
- Symmetry-based uncertainty


..unless data indicates otherwise?
Just as relevant in classical Euclidean setting
Geometric learning: right technical language for studying this
Geometric deep learning: models
Models:
- Graph convolutional neural networks
- Attention and graph transformers
- Invariant and equivariant networks
- Lots of other ideas
Check out the recent book, available with slides and other content at https://geometricdeeplearning.com
Applications
of Geometric Learning
Applications
: drug discovery
Graph neural network: predicted antibiotic activity in halicin, prev. studied for diabetes
Shown in mice to have broad-spectrum antibiotic activity
Figure and results: Stokes et al. (Cell, 2020)
Applications: recommendation systems
Graph neural networks: used to improve complementary product recommendation
Improved performance in production compared to Amazon's prior approach
Figure and results: Hao et al. (CIKM 2020)
Applications: traffic prediction
Graph neural networks: Google Maps traffic ETA prediction
Improved accuracy in production compared to prior approach
Figure and results: Derrow-Pinion et al. (CIKM 2021)
ProbAI 2025
Geometric Probabilistic Models
Viacheslav (Slava) Borovitskiy
https://vab.im
Part I: background, motivation, technical fundamentals
- Model-based decision-making
- Probabilistic modeling and uncertainty
- Digression: Gaussian processes, the "gold standard"
- Geometric learning: working with structured data
Part II: geometric probabilistic models
- Example problem: Setup
- Basic types of probabilistic models
- Example problem: Evaluation
- Emerging applications
- Software
- Summary
References
Example problem: Setup
An example problem
San Jose highway network: graph with 1016 nodes
325 labeled nodes with known traffic speed in miles per hour
Use 250 labeled nodes for training data and 75 for test data
Dataset details: Borovitskiy et al. (AISTATS 2021)
Basic types of probabilistic models
Basic types of probabilistic models
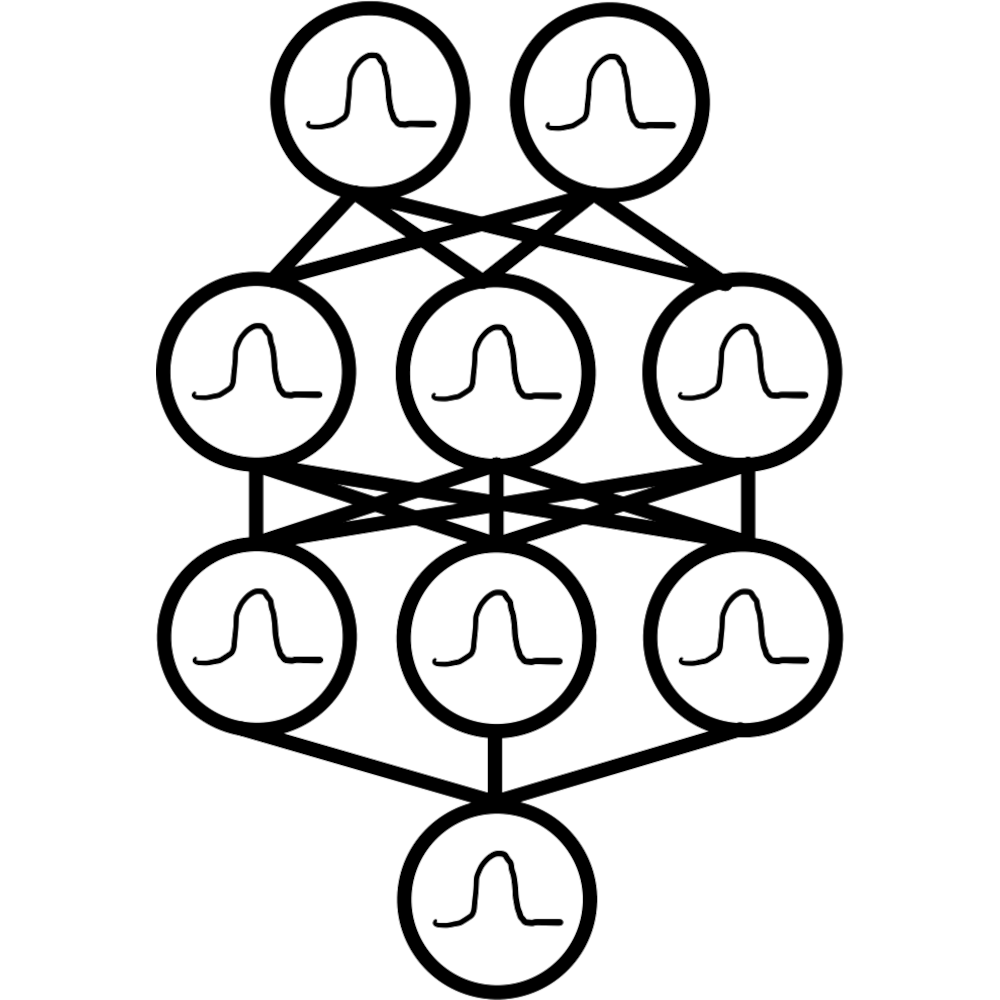
Bayesian neural networks
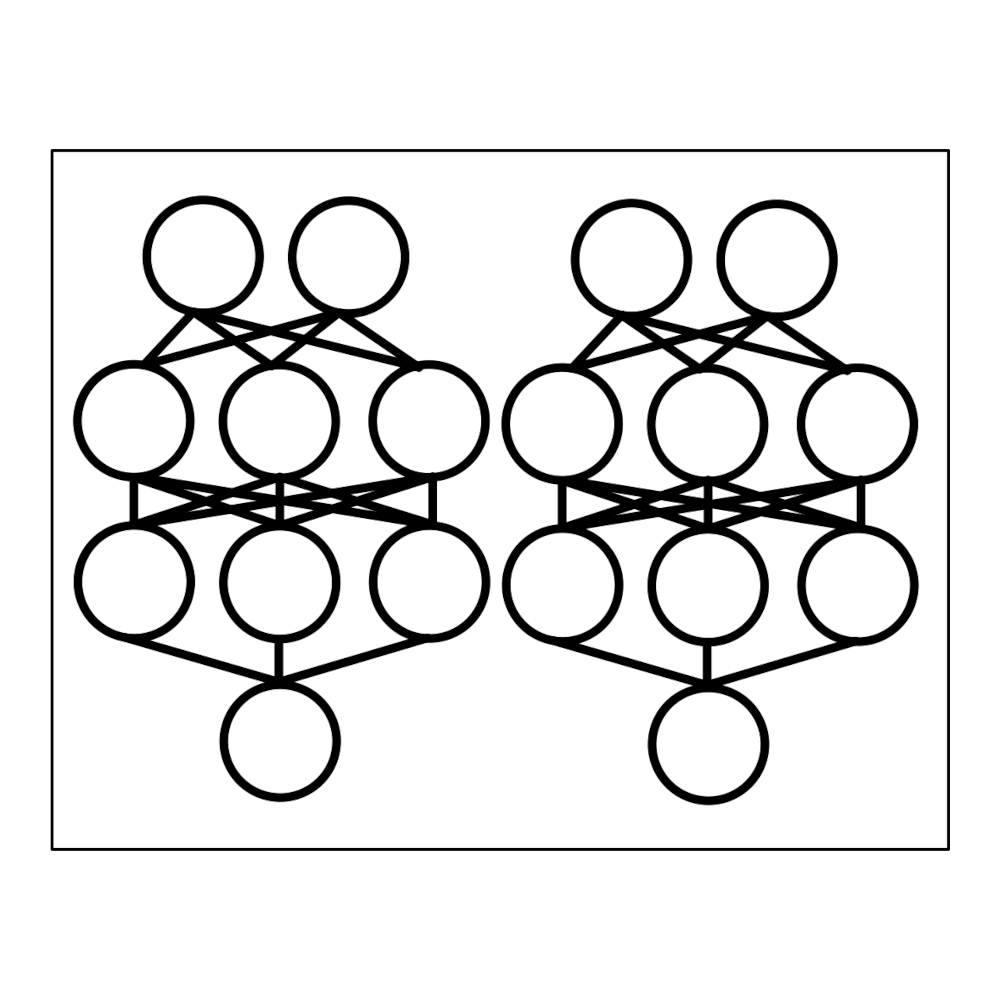
Deep ensembles
$\underbrace{\hphantom{\text{Bayesian Neural Networks}\qquad{Deep ensembles}}}_{\text{require specialized architectures}}$
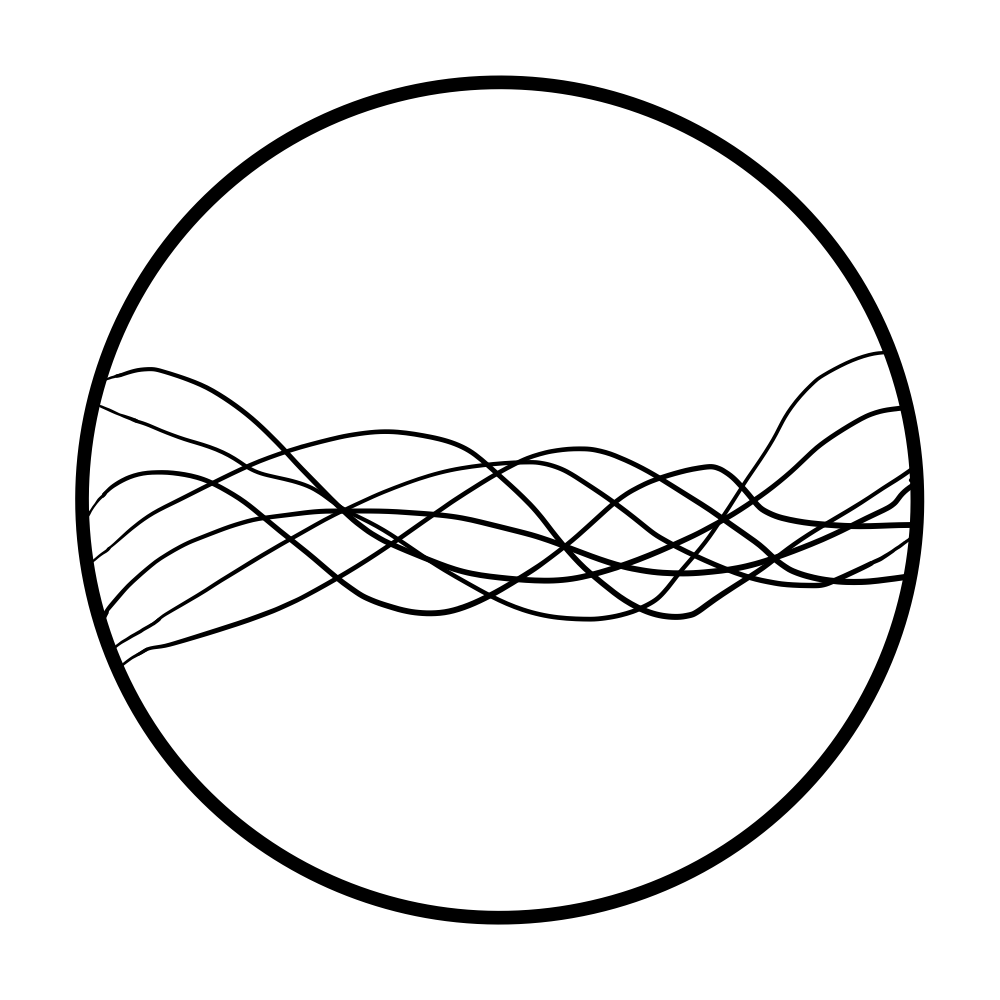
Gaussian processes
$\underbrace{\hphantom{\text{Gaussian Processes}}}_{\text{require specialized kernels}}$
Graph convolutional neural networks (Graph CNNs)
Base setting: $f: X \to Y$, where both $X$ and $Y$ are spaces of graphs.
- Let $\m{A}$ be a $d \x d$ weighted adjacency matrix.
-
Let $\m{X}$ be the $d \x m$ matrix of node features:
— $\v{x}_{i} = (\m{X}_{i 1}, \ldots, \m{X}_{i m})$ is the feature vector of node $i$.
A graph convolutional layer computes a new $d \x m'$ matrix of node features:
$$ \htmlData{class=fragment}{ \v{x}_{i}' = \f{ReLu} (\m{W} \v{z}_{i}) } \htmlData{class=fragment}{ \qquad \v{z}_{i} = \sum_{j \in \c{N}(i) \cup \cbr{i}} \frac{\m{A}_{i j}}{\sqrt{(1 + d_i) (1 + d_j)}} \v{x}_j } $$where $\m{W}$ are trainable weights, $d_i$ are degrees and $\c{N}(i)$ are neighbor sets.
Graph convolutional neural networks (Graph CNNs)
Graph convolutional neural networks for node regression
Set $\v{x}_i$ to be, e.g., either of
- constant: $\m{x}_i = (1, \ldots, 1)$;
- index $i$ zero-one encoded: $\m{x}_i = (0, \ldots, 1, \ldots, 0)$;
- masked targets: $\m{x}_i = y_i$ if known, $\m{x}_i = 0$ otherwise.
Resulting model $f_{\theta}$ maps $\m{X}$ to $\v{y}$.
Take some loss $L(\cdot, \cdot)$ and train by solving
$$ \htmlData{class=fragment}{ \argmin_{\theta} \sum_{i \in \text{observed nodes}} L(f_{\theta}(\v{X})_i, y_i) . } $$Graph Gaussian processes
$$ k_{\kappa, \sigma^2}(x,x') = \sigma^2\exp\del{-\frac{|x - x'|^2}{2\kappa^2}} $$
$$ k_{\kappa, \sigma^2}^{(d)}(x,x') = \sigma^2\exp\del{-\frac{d(x,x')^2}{2\kappa^2}} $$
where $d$ is the shortest path distance on a given graph $G$.
Graph nodes: not well-defined unless $G$ can be isometrically embedded into a Hilbert space.
Schoenberg (Trans. Am. Math. Soc. 1938).
Not well-defined on the square graph.
Graph Gaussian processes
Another characterization of $k_{\kappa, \sigma^2}$ in terms of the Laplacian $\Delta$:
$k_{\kappa, \sigma^2} \propto \sigma^2 \exp(-\frac{\kappa^2}{2} \Delta)$ .
On graphs: use graph Laplacian. $k_{\kappa, \sigma^2}$ is known as heat/diffusion kernel.
Claim. $k_{\kappa, \sigma^2}$ is positive definite, "stationary" and "smooth".
$k_{\kappa, \sigma^2}$ can be made explicit:
$$ \htmlData{class=fragment}{ k_{\kappa, \sigma^2}(i, j) = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^{\abs{V}-1} e^{-\frac{\kappa^2}{2}\lambda_n} \mathbf{f}_n(i)\mathbf{f}_n(j) } $$where $\lambda_n, f_n$ are eigenvalues and eigenvectors of the graph Laplacian $\Delta$.
Example problem: Evaluation
Simple baseline
Simple baseline
: prediction
: uncertainty
Trying out different probabilistic models
Trying out different probabilistic models
Link to code at the end of the tutorial
Sanity check:
Deterministic graph CNN
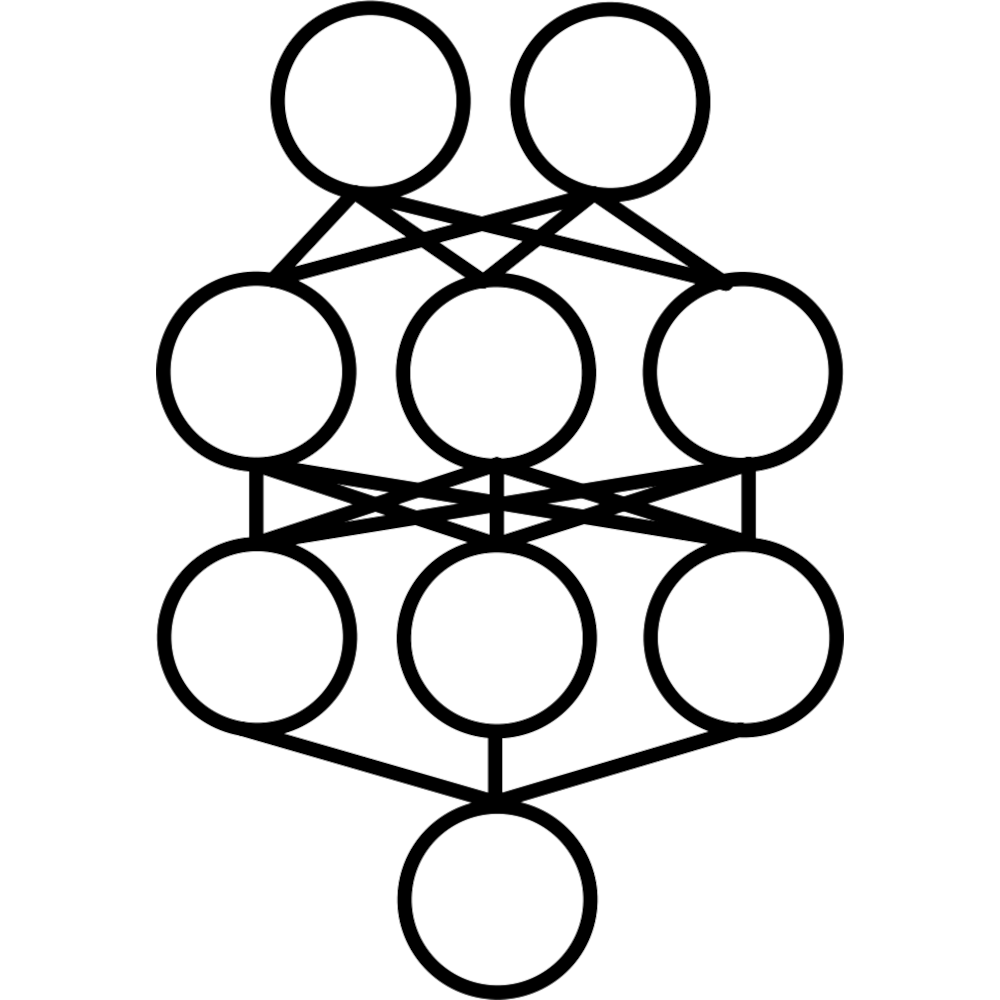
Deterministic graph CNN
: prediction (1 layer)
: prediction (7 layers)
Probabilistic models
Deep ensemble

Graph CNN ensembles: Practice
Deep ensembles:
- Train $K$ neural networks $f_1, \ldots, f_K$ with different initializations.
- Prediction: average $f(x) = \frac{1}{K} \sum_{k=1}^K f_k(x)$.
- Uncertainty: std deviation $\sigma(x) = (\frac{1}{K} \sum_{k=1}^K (f_k(x) - f(x))^2)^{1/2}$.
Open Notebook 2 [Google Colab]
at https://vab.im/probai2025/.
Compute RMSE and NLL of the ensemble.
Deep ensemble
: prediction
: uncertainty
Bayesian graph CNN

Bayesian graph CNN
: prediction (100 neurons/layer)
: uncertainty (100 neurons/layer)
: prediction (10 neurons/layer)
: uncertainty (10 neurons/layer)
Gaussian process

Gaussian process
: geometric Matérn kernel
– prediction
– uncertainty
Not all Gaussian processes
work well
Gaussian process
: geometric Matérn kernel, uncertainty
: random walk kernel, uncertainty
: inverse cosine kernel, uncertainty
A way to think about this
A way to think about this
This example: easy-to-use and visualize benchmark for probabilistc regression on geometric data
Geometric Gaussian processes:
- Reliable off-the-shelf probabilistic models
- Solid baselines to benchmark other models against
Gaussian processes:
other geometric settings
Gaussian processes:
other geometric settings

Simple manifolds:
meshes, spheres, tori
Borovitskiy et al. (AISTATS 2020)

Compact Lie groups and
homogeneous spaces:
$\small\f{SO}(n)$, resp. $\small\f{Gr}(n, r)$
Azangulov et al. (JMLR 2024)
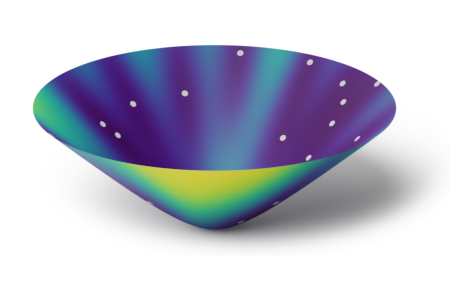
Non-compact symmetric
spaces: $\small\bb{H}_n$ and $\small\f{SPD}(n)$
Azangulov et al. (JMLR 2024)
Gaussian processes: other geometric settings

Vector fields on simple manifolds
Robert-Nicoud et al. (AISTATS 2024)
Gaussian processes: other geometric settings
Edges of graphs
Yang et al. (AISTATS 2024)
Metric graphs
Bolin et al. (Bernoulli 2024)
Cellular Complexes
Alain et al. (ICML 2024)
Spaces of Graphs
Borovitskiy et al. (AISTATS 2023)
Implicit geometry
Semi-supervised learning:
scalar functions
Fichera et al. (NeurIPS 2023)

Semi-supervised learning:
vector fields
Peach et al. (ICLR 2024)
GeometricKernels: RBF (heat) and Matérn kernels on geometric domains
https://geometric-kernels.github.io/
Emerging real-world applications
Robotics: Bayesian optimization of control policies
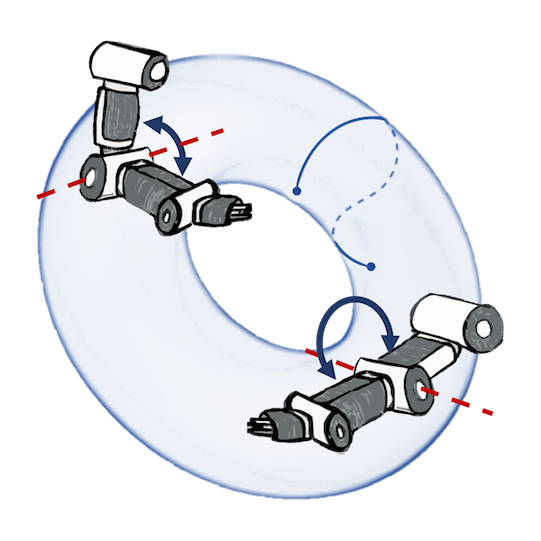
Joint postures: $\mathbb{T}^d$
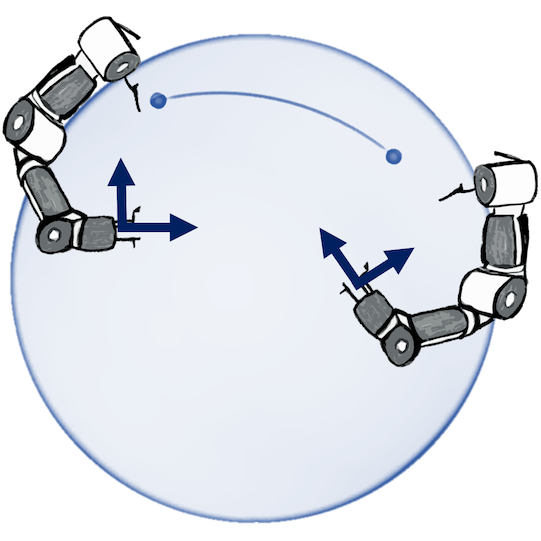
Rotations: $\mathbb{S}_3$, $\operatorname{SO}(3)$
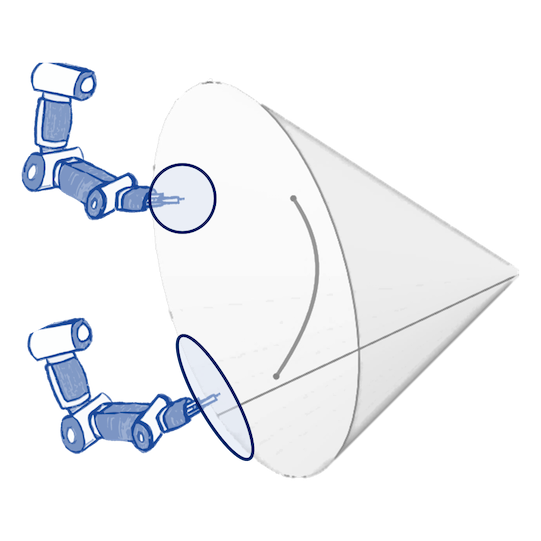
Manipulability: $\operatorname{SPD(3)}$
Jaquier et al. (CoRL 2019, CoRL 2021), figures by the authors
Medicine: probabilistic atrial activation maps
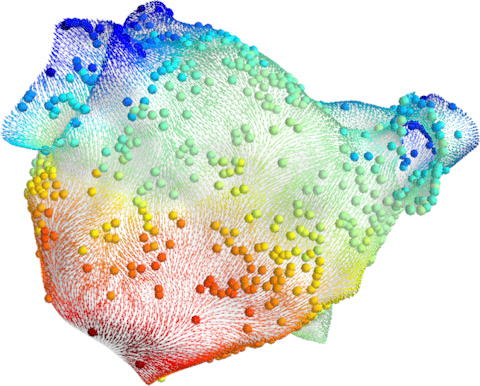
Prediction
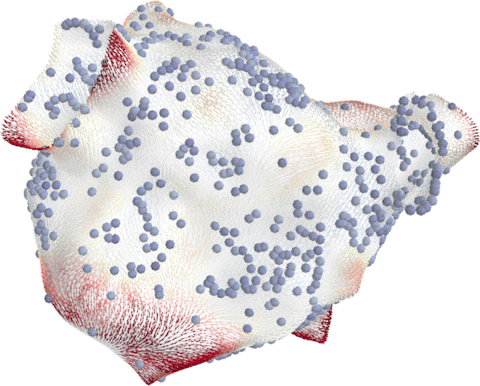
Uncertainty
Matérn Gaussian processes on meshes (independently proposed)
Coveney et al. (TBE 2019, PTRSA 2020), figures by the authors
Engineering: Bayesian optimization of shapes
Based on ensembles of geodesic CNNs
Neural Concept, video from neuralconcept.com
Software
Materials: Software stack
Stack:
- PyTorch Geometric: graph neural networks
- Pyro: probabilistic programming
- GPyTorch: Gaussian processes
- GeometricKernels: geometric Matérn kernels
Software and frameworks
| PyTorch | JAX | TensorFlow | |
|---|---|---|---|
| Graph Neural Networks | PyTorch Geometric | Jraph | TensorFlow GNN |
| Probabilistic Programming | Pyro | NumPyro | TensorFlow Probability |
| Gaussian Processes | GPyTorch | GPJax | GPflow |
| Geometric Kernels | GeometricKernels | ||
Neural networks beyond the graph setting: various small libraries
Summary
Summary
Geometric machine learning: increasingly popular
- Waves: kernels on structured data, geometric deep learning
Geometric probabilistic models: emerging research area
- Geometric probabilistic > geometric + probabilistic
- Geometric Gaussian processes: solid off-the-shelf baselines

Thank you!
https://vab.im/probai2025
Thank you!
https://vab.im/probai2025
References
References: geometric deep learning and applications
M. M. Bronstein, J. Bruna, T. Cohen, and P. Veličković. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. Available at: https://geometricdeeplearning.com, 2021.
J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz, N. M. Donghia, C. R. MacNair, S. French, L. A. Carfrae, Z. Bloom-Ackermann, V. M. Tran, A. Chiappino-Pepe, A. H. Badran, I. W. Andrews, E. J. Chory, G. M. Church, E. D. Brown, T. S. Jaakkola, R. Barzilay, and J. J. Collins. A deep learning approach to antibiotic discovery. Cell, 2020.
J. Hao, T. Zhao, J. Li, X. L. Dong, C. Faloutsos, Y. Sun, and W. Wang. P-companion: A principled framework for diversified complementary product recommendation. Conference on Information and Knowledge Management, 2020.
A. Derrow-Pinion, J. She, D. Wong, O. Lange, T. Hester, L. Perez, M. Nunkesser, S. Lee, X. Guo, B. Wiltshire, P. W. Battaglia, V. Gupta, A. Li, Z. Xu, A. Sanchez-Gonzalez, Y. Li, and P. Veličković. ETA prediction with graph neural networks in Google Maps. Conference on Information and Knowledge Management, 2021.
References: probabilistic neural networks in geometic settings
Y. Zhang, S. Pal, M. Coates, and D. Ustebay. Bayesian graph convolutional neural networks for semi-supervised classification. AAAI Conference on Artificial Intelligence, 2019.
M. Stadler, B. Charpentier, S. Geisler, D. Zügner, and S. Günnemann. Graph posterior network: Bayesian predictive uncertainty for node classification. Advances in Neural Information Processing Systems, 2021.
H. Shi, X. Zhang, S. Sun, L. Liu, and L. Tang. A survey on Bayesian graph neural networks. Intelligent Human-Machine Systems and Cybernetics, 2021.
A. Hasanzadeh, E. Hajiramezanali, S. Boluki, M. Zhou, N. Duffield, K. Narayanan, and X. Qian. Bayesian graph neural networks with adaptive connection sampling. International Conference on Machine Learning, 2020.
N. Durasov, A. Lukoyanov, J. Donier, and P. Fua. DEBOSH: Deep bayesian shape optimization. Technical Report: Neural Concept, 2021.
Q. Wang, S. Wang, D. Zhuang, H. Koutsopoulos, and J. Zhao. Uncertainty quantification of spatiotemporal travel demand with probabilistic graph neural networks. IEEE Transactions on Intelligent Transportation Systems, 2024.
L. Kahle and F. Zipoli. Quality of uncertainty estimates from neural network potential ensembles. Physical Review E, 2022.
References: geometric Gaussian processes
V. Borovitskiy, I. Azangulov, A. Terenin, P. Mostowsky, M. P. Deisenroth, and N. Durrande. Matérn Gaussian Processes on Graphs. Artificial Intelligence and Statistics, 2021.
A. Feragen, F. Lauze, and S. Hauberg. Geodesic exponential kernels: When curvature and linearity conflict. Computer Vision and Pattern Recognition, 2015.
I. J. Schoenberg. Metric spaces and positive definite functions. Transactions of the American Mathematical Society, 1938.
P. Whittle. Stochastic-processes in several dimensions. Bulletin of the International Statistical Institute, 1963.
F. Lindgren, H. Rue, and J. Lindström. An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. Journal of the Royal Statistical Society, Series B: Statistical Methodology, 2011.
V. Borovitskiy, A. Terenin, P. Mostowsky, and M. P. Deisenroth. Matérn Gaussian Processes on Riemannian Manifolds. Advances in Neural Information Processing Systems, 2020.
I. Azangulov, A. Smolensky, A. Terenin, and V. Borovitskiy. Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces I: the compact case. Journal of Machine Learning Research, 2024.
I. Azangulov, A. Smolensky, A. Terenin, and V. Borovitskiy. Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces II: non-compact symmetric spaces, 2024.
D. Robert-Nicoud, A. Krause, and V. Borovitskiy. Intrinsic Gaussian Vector Fields on Manifolds. Artificial Intelligence and Statistics, 2024.
M. Yang, V. Borovitskiy, and E. Isufi. Hodge-Compositional Edge Gaussian Processes. Artificial Intelligence and Statistics, 2024.
D. Bolin, A. B. Simas, and J. Wallin. Gaussian Whittle-Matérn fields on metric graphs. Bernoulli, 2024.
M. Alain, S. Takao, B. Paige, and M. P. Deisenroth. Gaussian Processes on Cellular Complexes. International Conference on Machine Learning, 2024.
References: geometric Gaussian processes
V. Borovitskiy, M. R. Karimi, V. R. Somnath, and A. Krause. Isotropic Gaussian Processes on Finite Spaces of Graphs. Artificial Intelligence and Statistics, 2023.
B. Fichera, V. Borovitskiy, A. Krause, and A. Billard. Implicit Manifold Gaussian Process Regression. Advances in Neural Information Processing Systems, 2023.
R. Peach, M. Vinao-Carl, N. Grossman, and M. David. Implicit Gaussian process representation of vector fields over arbitrary latent manifolds. International Conference on Learning Representations, 2024.
D. Li, W. Tang, and S. Banerjee. Inference for Gaussian Processes with Matern Covariogram on Compact Riemannian Manifolds. Journal of Machine Learning Research, 2023.
P. Rosa, V. Borovitskiy, A. Terenin, and J. Rousseau. Posterior Contraction Rates for Matérn Gaussian Processes on Riemannian Manifolds. Advances in Neural Information Processing Systems, 2023.
N. Jaquier, V. Borovitskiy, A. Smolensky, A. Terenin, T. Asfour, and L. Rozo. Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels. Conference on Robot Learning, 2021.
N. Jaquier, L. Rozo, S. Calinon, and M. Bürger. Bayesian optimization meets Riemannian manifolds in robot learning. Conference on Robot Learning, 2020.
S. Coveney, C. Corrado, C. H. Roney, R. D. Wilkinson, J. E. Oakley, F. Lindgren, S. E. Williams, M. D. O'Neill, S. A. Niederer, and R. H. Clayton. Probabilistic interpolation of uncertain local activation times on human atrial manifolds. IEEE Transactions on Biomedical Engineering, 2019.
S. Coveney, C. Corrado, C. H. Roney, D. OHare, S. E. Williams, M. D. O'Neill, S. A. Niederer, R. H. Clayton, J. E. Oakley, and R. D. Wilkinson. Gaussian process manifold interpolation for probabilistic atrial activation maps and uncertain conduction velocity. Philosophical Transactions of the Royal Society A, 2020.