Uncertainty in multivariate, non-Euclidean,
Gaussian Processes
Gaussian Processes
Uncertainty-enabled models: input ⟶ prediction + uncertainty.
Gaussian processes (GPs) — gold standard.
— random functions with jointly Gaussian marginals.
Bayesian learning: prior GP + data = posterior GP
Prior GPs are determined by kernels (covariance functions)
— have to be positive semi-definite (PSD),
— not all kernels define "good" GPs.
This talk: defining priors / kernels.
General-purpose GPs
On $\mathbb{R}^d$: Matérn Gaussian Processes
$$
\htmlData{class=fragment fade-out,fragment-index=6}{
\footnotesize
\mathclap{
k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}
}
}
\htmlData{class=fragment d-print-none,fragment-index=6}{
\footnotesize
\mathclap{
k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\norm{x-x'}^2}{2\kappa^2}}
}
}
$$
$\sigma^2$: variance
$\kappa$: length scale
$\nu$: smoothness
$\nu\to\infty$: RBF kernel (Gaussian, Heat, Diffusion)
$\nu = 1/2$
$\nu = 3/2$
$\nu = 5/2$
$\nu = \infty$
Work very well for inputs in $\R^d$,
at least for small $d$.
Non-Euclidean Domains

Manifolds
e.g. in physics (robotics)
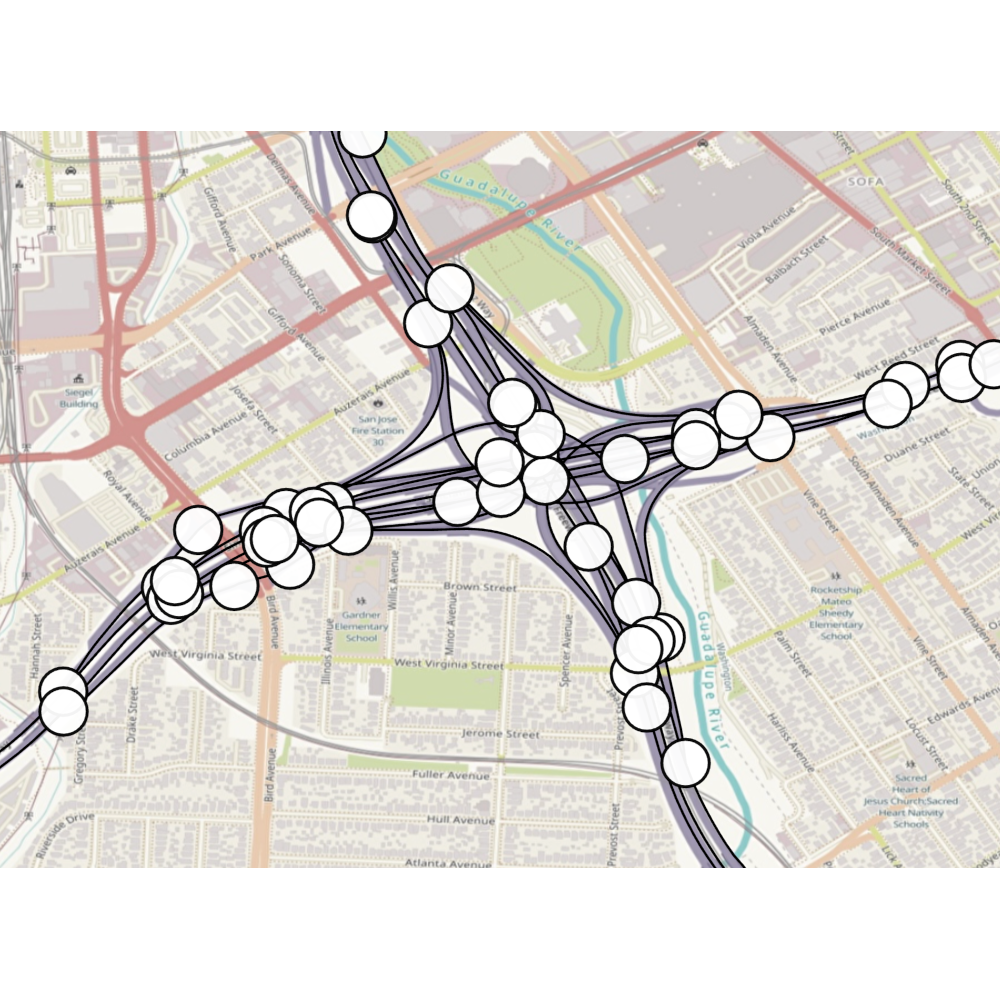
Graphs
e.g. for road networks
Spaces of graphs
e.g. for drug design
General-purpose GPs beyond $\mathbb{R}^d$
How to Generalize the RBF Kernel?
$$ k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2\exp\del{-\frac{|x - x'|^2}{2\kappa^2}} $$
$$ k_{\infty, \kappa, \sigma^2}^{(d)}(x,x') = \sigma^2\exp\del{-\frac{d(x,x')^2}{2\kappa^2}} $$
Manifolds: not PSD for some $\kappa$ (in some cases—for all) unless the manifold is isometric to $\mathbb{R}^d$.
Feragen et al. (CVPR 2015) and Da Costa et al. (Preprint 2023).
Graph nodes: not PSD for some $\kappa$ unless can be isometrically embedded into a Hilbert space.
Schoenberg (Trans. Am. Math. Soc. 1938).
Not PSD on the square graph.
Not PSD on the circle manifold.
A Well-defined Generalization of the RBF Kernel
On $\mathbb{R}^d$, we have $$ k_{\infty, \kappa, \sigma^2}(x, x') \propto \mathcal{P}(\kappa^2/2, x, x'), $$ where $\mathcal{P}$ is the heat kernel, i.e. the solution of $$ \frac{\partial \mathcal{P}}{\partial t}(t, x, x') = \Delta_x \mathcal{P}(t, x, x') \qquad \mathcal{P}(0, x, x') = \delta_x(x') $$ Alternative generalization: use the above as the definition of the RBF kernel.
☺ Always positive semi-definite + Simple and general inductive bias.
☹ Implicit, requires solving the equation.
Generalizing Matérn Kernels
Matérn kernels $k_{\nu, \kappa, \sigma^2}$ can be defined whenever $\mathcal{P}(t, x, x')$ is defined:
$$ k_{\nu, \kappa, \sigma^2}(x, x') \propto \sigma^2 \int_{0}^{\infty} t^{\nu-1+d/2}e^{-\frac{2 \nu}{\kappa^2} t} \mathcal{P}(t, x, x') \mathrm{d} t $$(there are other—usually equivalent—definitions)
☺ Always positive semi-definite + Simple and general inductive bias.
☹ Implicit.
Making Matérn Kernels Explicit
For example, on a compact Riemannian manifold of dimension $d$: $$ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^\infty \Phi_{\nu, \kappa}(\lambda_n) f_n(x) f_n(x') $$
$\lambda_n, f_n$: eigenvalues and eigenfunctions of the Laplace–Beltrami operator
$$ \htmlData{fragment-index=4,class=fragment}{ \Phi_{\nu, \kappa}(\lambda) = \begin{cases} \htmlData{fragment-index=5,class=fragment}{ \del{\frac{2\nu}{\kappa^2} - \lambda}^{-\nu-\frac{d}{2}} } & \htmlData{fragment-index=5,class=fragment}{ \nu < \infty \text{ --- Matérn} } \\ \htmlData{fragment-index=6,class=fragment}{ e^{-\frac{\kappa^2}{2} \lambda} } & \htmlData{fragment-index=6,class=fragment}{ \nu = \infty \text{ --- RBF (Heat)} } \end{cases} } $$Vector Fields: What and Why?
Motivating Examples
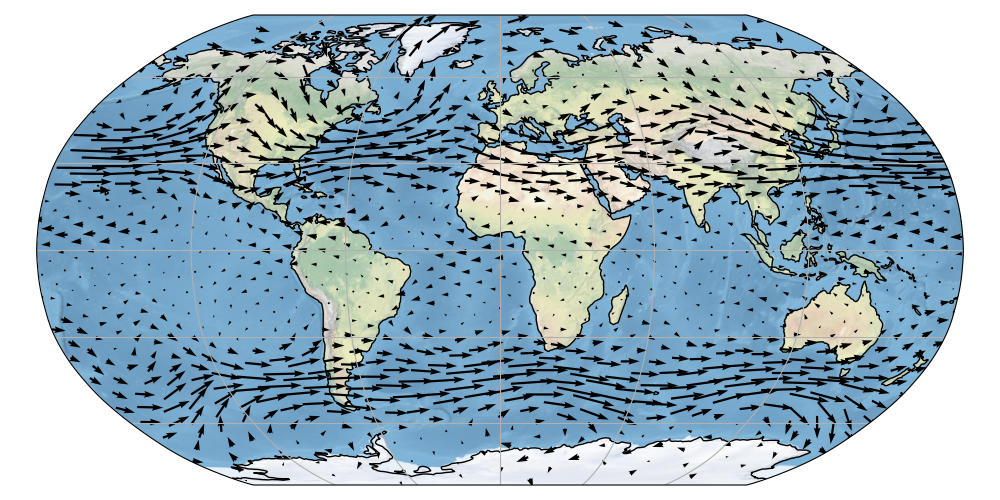
Wind velocities (actually, live on the sphere $\mathbb{S}_2$)
Also:
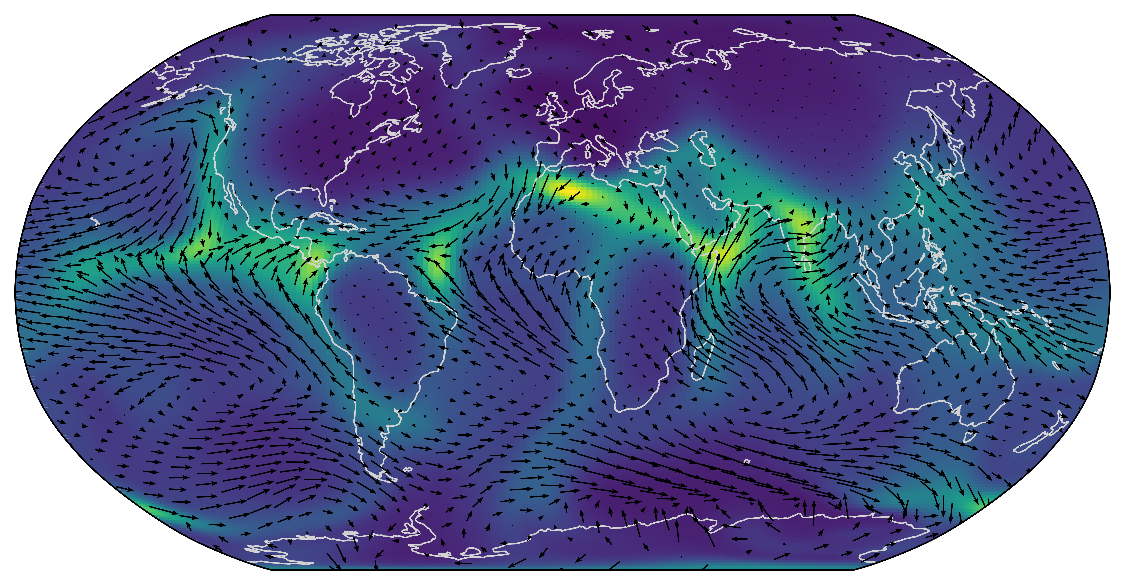
- Ocean currents (actually, live on the subset of the sphere $\mathbb{S}_2$)
- Force fields of a dynamical systems (often live on manifolds, e.g. on hypertori $\mathbb{T}^d$)
Vector Fields vs Vector-valued Functions
Euclidean case: vector field = vector-valued function.
On manifolds: vector-valued functions with outputs tangent to the manifold.

Vector function
(not tangent)

Vector field
(tangent)
Simple and General:
Projected Gaussian Processes
Projected Gaussian Processes
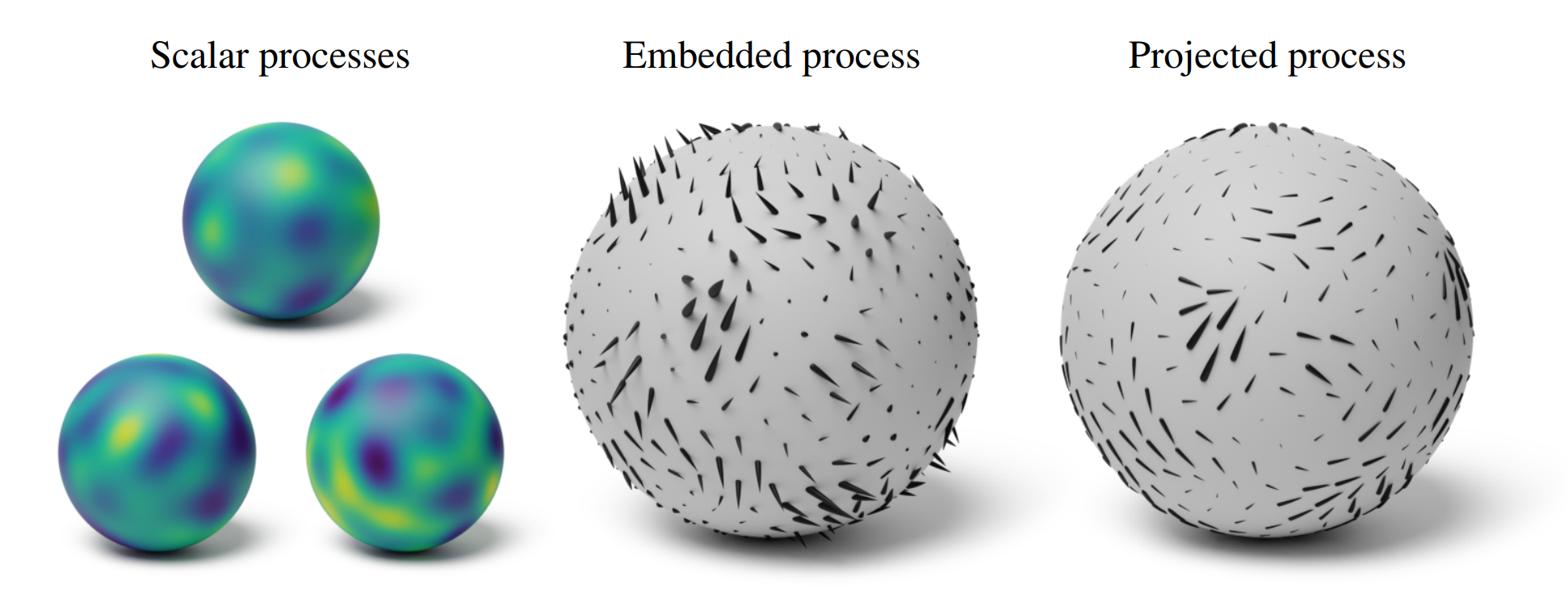
Projected Gaussian Processes—simple and general Gaussian vector fields (GVFs).
ERA5 Data
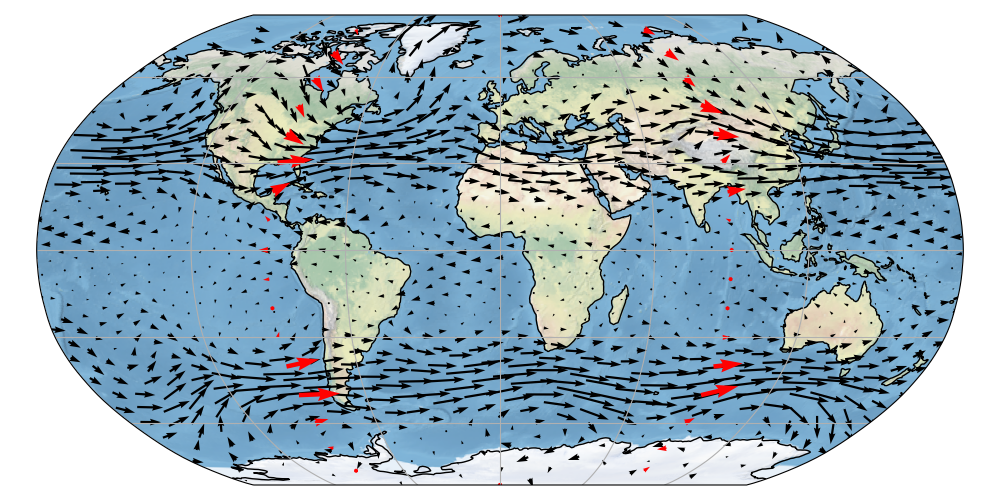
Ground truth with observations (red)
Experimental Results: projected GPs perform quite well.
Projected Gaussian Processes—The Issue

Fit on a single observation ($\kappa \to \infty$).
Non-monotonic uncertainty!
Projected Gaussian Processes—The Issue

Fit on a single observation ($\kappa \to \infty$).
Non-monotonic uncertainty!
Projected Gaussian Processes—The Issue

Fit on a single observation ($\kappa \to \infty$).
Non-monotonic uncertainty!
Going Principled:
Hodge–Matérn Gaussian Vector Fields
Hodge–Matérn Gaussian Vector Fields
Hodge theory: heat equation on vector fields.
Define $ k_{\infty, \kappa, \sigma^2}(x, x') \propto \mathcal{P}(\kappa^2/2, x, x'), $ where $$ \frac{\partial \mathcal{P}}{\partial t}(t, x, x') = \Delta_x \mathcal{P}(t, x, x') \qquad \mathcal{P}(0, x, x') = \delta_x(x') $$ and $\Delta$ is the Hodge Laplacian.
Define Matérn GVFs in terms of $\mathcal{P}$ in the usual way.
Making Hodge–Matérn Gaussian Vector Fields Explicit
Specifically, on a compact oriented Riemannian manifold $M$ of dimension $d$: $$ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^\infty \Phi_{\nu, \kappa}(\lambda_n) s_n(x) \otimes s_n(x') $$
$\lambda_n, s_n$: eigenvalues and eigenfields of the Hodge Laplacian.
$$ \htmlData{fragment-index=4,class=fragment}{ \Phi_{\nu, \kappa}(\lambda) = \begin{cases} \htmlData{fragment-index=5,class=fragment}{ \del{\frac{2\nu}{\kappa^2} - \lambda}^{-\nu-\frac{d}{2}} } & \htmlData{fragment-index=5,class=fragment}{ \nu < \infty \text{ --- Matérn} } \\ \htmlData{fragment-index=6,class=fragment}{ e^{-\frac{\kappa^2}{2} \lambda} } & \htmlData{fragment-index=6,class=fragment}{ \nu = \infty \text{ --- RBF (Heat)} } \end{cases} } $$Open Problem #1:
How to compute eigenfields $s_n$ on $\mathbb{S}_d$ with $d > 2$?
Context: On $\mathbb{S}_2$, $\nabla f_n$ and $\star \nabla f_n$ form the basis of orthogonal eigenfields ($\star$—$90^{\circ}$ rotation).
Motivation: deep Gaussian processes (later).

Projected Matérn GP.

Projected Matérn GP, rotated.

Hodge–Matérn GVF.
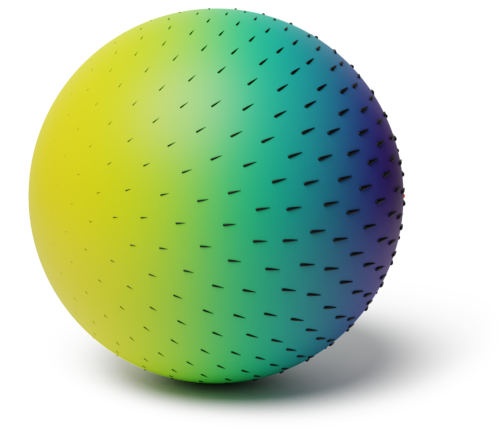
Hodge–Matérn GVF, rotated.
Bonus: Divergence- and Curl-free Fields
In $2$-D, each $s_n$ is either divergence-free, curl-free, or both (harmonic).

Curl-free eigenfield $s_n$.

Rotate it: div-free eigenfield $s_l$.
Only use one type: kernels $k_{\nu, \kappa, \sigma^2}^{\text{div-free}}$, $k_{\nu, \kappa, \sigma^2}^{\text{curl-free}}$, $k_{\nu, \kappa, \sigma^2}^{\text{harm}}$.
Hodge-compositional kernel: fit $\alpha, \beta, \gamma$ and $\kappa_1, \kappa_2, \kappa_3$ in
$$ k_{\nu,\kappa_1, \alpha}^{\text{div-free}} + k_{\nu, \kappa_2, \beta}^{\text{curl-free}} + k_{\nu, \kappa_3, \gamma}^{\text{harm}} $$
ERA5 Experimental results
| Kernel | MSE | NLL |
|---|---|---|
| Pure noise | 2.07 | 2.89 |
| Projected Matérn | 1.39 | 2.33 |
| Hodge–Matérn | 1.67 | 2.58 |
| div-free Hodge–Matérn | 1.10 | 2.16 |
| Hodge-compositional Matérn | 1.09 | 2.16 |
Hodge-compositional Matérn does best and is the easiest to use.
Open Problem #2:
Connection Laplacian instead of Hodge Laplacian.
What changes?
How to compute kernels?
A Far-reaching Application of GVF:
Residual Deep Gaussian Processes
Residual Deep Gaussian Processes
GVFs allow building deep GPs on manifolds without the need for manifold-to-manifold layers.
Wyrwal et al. (ICLR 2025)
Bayesian Optimization (BO) with Residual Deep Gaussian Processes

Irregular benchmark function.
Bayesian optimization performance.
Open Problem #3:
Manifold deep GPs for BO in real-world robotics.
Context: Jaquier et al. (2022) used manifold Matérn GPs for optimizing robotics control policies.
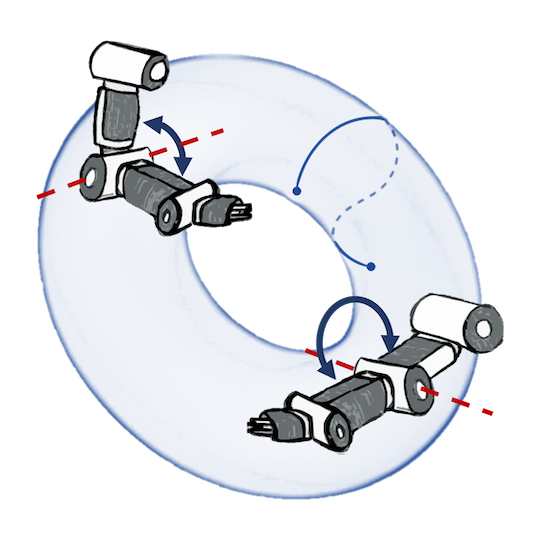
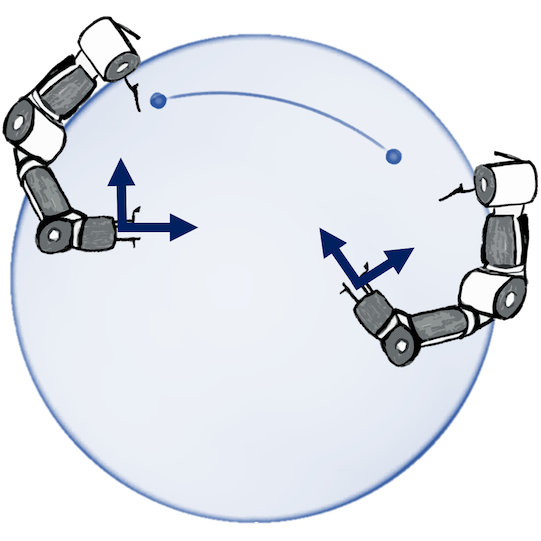
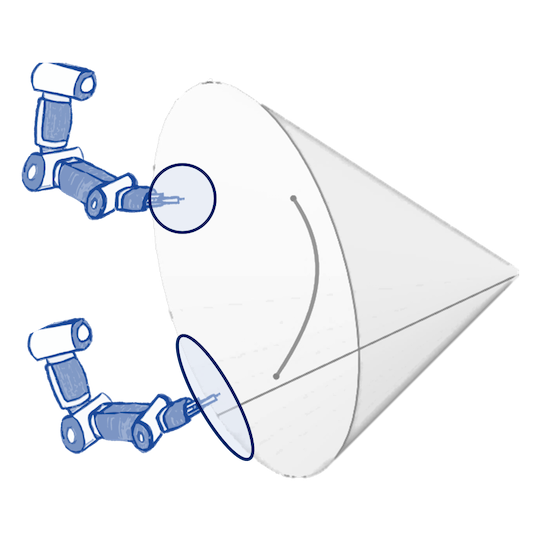
Weather Modeling with Residual Deep Gaussian Processes
Mean prediction & uncertainty of the GVF. Uncertainty depends on $y$-s!
Performs much better than a shallow GVF for denser data.
Open Problem #4:
Manifold deep GPs for faster VI for Euclidean data.
Context: Dutordoir et al. (2020) suggested mapping Euclidean data to the hypersphere and using GPs on $\mathbb{S}_d$. There, manifold Fourier feature enable faster variational inference (VI).
State-of-the-art: Wyrwal et al. (2025) tried doing the same for deep GPs based on projected GPs.
- Variational inference converges faster.
- Resulting performance drops significantly.
Maybe use Hodge GVFs (see open problem #1) or different maps $\mathbb{R}^d \to \mathbb{S}_{d'}$?
Last Note on Smooth Vector Fields
Going Discrete:
Flows Over Graph Edges
Flows Over Graph Edges
: Discrete Vector Fields
Let $M$ be a manifold and $G = (V, E)$ a graph.
Simplest way to see the connection: consider the gradient $f = \nabla g$.
- For $g: M \to \mathbb{R}$, $f$ is a vector field (1-form).
-
For $g: V \to \mathbb{R}$, $f$ is an alternating edge function (1-chain).
$(\nabla g)(e) = g(x') - g(x)$ where $e = (x, x') \in E$.
Alternating function: $f(e) = -f(-e)$ where $-e = (x', x)$.
Main idea: alternating functions on edges are analogous to vector fields.
Divergence and Curl
We can define divergence of an alternating edge function $f$ as $$ (\operatorname{div} f)(x) = - \sum_{x' \in N(x)} f((x, x')) \qquad x \in V $$ where $N(x)$ is the set of neighbors of $x$.
But how to define curl?
A Richer Structure: Simplicial 2-complexes
Take a graph $G = (V, E)$ and add an additional set of triangles $T$:
For each $t \in T$, $t = (e_1, e_2, e_3)$ is a triangle with edges $e_1, e_2, e_3 \in E$.
Simplicial 2-complex
Can also be extended beyond triangles: cellular complexes.
Hodge Theory on Simplicial 2-complexes
Curl of an alternating edge function $f$ (mind the orientations/signs)
$$ (\operatorname{curl} f)(t) = \sum_{e \in t} f(e) \qquad t \in T. $$
Can also define Hodge Laplacian matrix $\m{\Delta}$ on simplicial 2-complexes.
It defines the heat kernel $\mathcal{P}$ and through it all Matérn kernels $k_{\nu, \kappa, \sigma^2}$.
Eigenvectors of $\m{\Delta}$ can be split into divergence-free, curl-free, and harmonic:
- Can define $k_{\nu, \kappa, \sigma^2}^{\text{div-free}}$, $k_{\nu, \kappa, \sigma^2}^{\text{curl-free}}$, $k_{\nu, \kappa, \sigma^2}^{\text{harm}}$.
- Can define the Hodge-compositional kernel.
Application: Ocean Currents
Ocean currents data
Toy Application: Arbitrage-free Currency Exchange Rates
Forex data
If $r^{i \to j}$ is the exhange rate between currency $i$ and currency $j$, then
$$r^{i \to j} r^{j \to k} = r^{i \to k}$$
This is curl-free condition for $\log r^{i \to j}$.
Hodge-compositional kernels can infer it from data.
Software
GeometricKernels: Matérn and heat kernels on geometric domains
https://geometric-kernels.github.io/
Currently: has graph edges☺, doesn't have Gaussian vector fields ☹.
Thank you!
Thank you!
References
References
M. Alain, S. Takao, B. Paige, and M. P. Deisenroth. Gaussian Processes on Cellular Complexes. International Conference on Machine Learning, 2024.
V. Borovitskiy, I. Azangulov, A. Terenin, P. Mostowsky, M. P. Deisenroth, and N. Durrande. Matérn Gaussian Processes on Graphs. Artificial Intelligence and Statistics, 2021.
V. Borovitskiy, A. Terenin, P. Mostowsky, and M. P. Deisenroth. Matérn Gaussian Processes on Riemannian Manifolds. Advances in Neural Information Processing Systems, 2020.
D. Bolin, A. B. Simas, and J. Wallin. Gaussian Whittle-Matérn fields on metric graphs. Bernoulli, 2024.
S. Coveney, C. Corrado, C. H. Roney, D. OHare, S. E. Williams, M. D. O'Neill, S. A. Niederer, R. H. Clayton, J. E. Oakley, and R. D. Wilkinson. Gaussian process manifold interpolation for probabilistic atrial activation maps and uncertain conduction velocity. Philosophical Transactions of the Royal Society A, 2020.
N. Da Costa, C. Mostajeran, J.-P. Ortega, and S. Said. Invariant kernels on Riemannian symmetric spaces: a harmonic-analytic approach. Preprint, 2023.
A. Feragen, F. Lauze, and S. Hauberg. Geodesic exponential kernels: When curvature and linearity conflict. Computer Vision and Pattern Recognition, 2015.
M. Hutchinson, A. Terenin, V. Borovitskiy, S. Takao, Y. W. Teh, M. P. Deisenroth. Vector-valued Gaussian Processes on Riemannian Manifolds via Gauge Independent Projected Kernels. Advances in Neural Information Processing Systems, 2021.
N. Jaquier, V. Borovitskiy, A. Smolensky, A. Terenin, T. Asfour, and L. Rozo. Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels. Conference on Robot Learning, 2021.
P. Mostowsky, V. Dutordoir, I. Azangulov, N. Jaquier, M. J. Hutchinson, A. Ravuri, L. Rozo, A. Terenin, V. Borovitskiy. The GeometricKernels Package: Heat and Matérn Kernels for Geometric Learning on Manifolds, Meshes, and Graphs. Preprint, 2024.
R. Peach, M. Vinao-Carl, N. Grossman, and M. David. Implicit Gaussian process representation of vector fields over arbitrary latent manifolds. International Conference on Learning Representations, 2024.
D. Robert-Nicoud, A. Krause, and V. Borovitskiy. Intrinsic Gaussian Vector Fields on Manifolds. Artificial Intelligence and Statistics, 2024.
I. J. Schoenberg. Metric spaces and positive definite functions. Transactions of the American Mathematical Society, 1938.
K. Wyrwal, A. Krause, and V. Borovitskiy. Residual Deep Gaussian Processes on Manifolds. International Conference on Learning Representations, 2025.
M. Yang, V. Borovitskiy, and E. Isufi. Hodge-Compositional Edge Gaussian Processes. Artificial Intelligence and Statistics, 2024.
Making Matérn Gaussian Vector Fields Explicit: the 2-D Case
Vector fields can be thought of as $1$-forms. $\Omega^k(M)$ is the space of $k$-forms.
Thm 1. $\Omega^k(M) = \operatorname{ker} \Delta \oplus \operatorname{im} \mathrm{d} \oplus \operatorname{im} \mathrm{d}^{\star}$, where
- $d: \Omega^k(M) \to \Omega^{k+1}(M)$ is exterior derivative,
- $d^{\star}: \Omega^{k+1}(M) \to \Omega^{k}(M)$ is the co-differential operator.
Thm 2. $d, d^{\star}$ map eigenforms to eigenforms, preserving orthogonality.
On $\mathbb{S}_2$: $\Omega^0(\mathbb{S}_2) = \Omega^2(\mathbb{S}_2)$ and the eigenforms are spherical harmonics,
On $\mathbb{S}_2$: $d$ is the gradient operator, $d^{\star}$ is gradient plus rotation by $90^{\circ}$.
Gaussian Vector Fields: The Formalism
Gaussian Vector Fields: The Formalism
Consider a vector-valued GP $\v{f}: \R^d \to \R^d$ and $\v{x}, \v{x}' \in \mathbb{R}^d$. Then $$ k(\v{x}, \v{x}') = \mathrm{Cov}(\v{f}(\v{x}), \v{f}(\v{x}')) \in \mathbb{R}^{d \x d} $$
For $x, x' \in M$ (a manifold), and $f$ a Gaussian vector field on $M$.
Hard to generalize the above:
$
f(x) \in T_x M \not= T_{x'} M \ni f(x')
.
$
Instead, for all $(x, v), (x', u) \in T M$, $$ k((x, u), (x', v)) = \mathrm{Cov}(\innerprod{f(x)}{v}_{T_x M}, \innerprod{f(x')}{u}_{T_{x'} M}) \in \mathbb{R} $$
Divergence and Curl
Fix orientation: for each $\{x, x'\} \in E$, choose either $(x, x')$ or $(x', x)$ to be positively oriented. Positively oriented edges can be enumerated by $\{1, .., |E|\}$.
Then, an alternating edge function $f$ can be represented by a vector $\v{f} \in \mathbb{R}^{|E|}$.
If $\m{B}_1$ is the oriented node-to-edge incidence matrix of dimension $|V| \x |E|$,
- $ \operatorname{grad} g = \m{B}_1^{\top} g, \qquad g \in \mathbb{R}^{|V|}, \qquad \operatorname{grad} g \in \mathbb{R}^{|E|}, $
- $ \operatorname{div} f = \m{B}_1 f, \qquad f \in \mathbb{R}^{|E|}, \qquad \operatorname{div} f \in \mathbb{R}^{|V|}. $
But how to define curl?
A Richer Structure: Simplicial 2-complexes
Take a graph $G = (V, E)$ and add an additional set of triangles $T$:
For each $t \in T$, $t = (e_1, e_2, e_3)$ is a triangle with edges $e_1, e_2, e_3 \in E$.
Simplicial 2-complex
Can also be extended beyond triangles: cellular complexes.
Hodge Theory on Simplicial 2-complexes
Let $\m{B}_2$ be an oriented edge-to-triangle incidence $|V| \x |T|$-matrix.
- Curl: $\operatorname{curl} f = \m{B}_2^{\top} f \in \mathbb{R}^{|E|}$.
- Hodge Laplacian: $\m{\Delta} = \m{B}_1^{\top} \m{B}_1 + \m{B}_2 \m{B}_2^{\top} \in \mathbb{R}^{|E| \x |E|}$.
It defines the heat kernel $\mathcal{P}$ and through it all Matérn kernels $k_{\nu, \kappa, \sigma^2}$.
Eigenvectors of $\m{\Delta}$ can be split into divergence-free, curl-free, and harmonic:
- Can define $k_{\nu, \kappa, \sigma^2}^{\text{div-free}}$, $k_{\nu, \kappa, \sigma^2}^{\text{curl-free}}$, $k_{\nu, \kappa, \sigma^2}^{\text{harm}}$.
- Can define the Hodge-compositional kernel.
Open Problem #5:
Implement Hodge Gaussian vecor Fields in GeometricKernels.
Also: Compare with Baselines
Implementation (Colab notebook) — clickable
Doesn't have Gaussian vector fields ☹. To be updated soon.
Open Problem #6:
Alternative geometric representations in the benchmark above.
Currently: graph nodes. Need also: graph edges, metric graph.