Motivation:
Model-based decision-making
Model-based decision-making
: Bayesian optimization
Automatic explore-exploit tradeoff
Principle of Separation:
modeling and decision-making
Learning with Uncertainty
Input ⟶ prediction + uncertainty.
Gaussian processes (GPs) — gold standard.
— random functions with jointly Gaussian marginals.
Bayesian learning: prior GP + data = posterior GP
Prior GPs are determined by kernels (covariance functions)
— have to be positive semi-definite,
— not all kernels define "good" GPs.
Standard GPs: Matérn Gaussian Processes
$$
\htmlData{class=fragment fade-out,fragment-index=6}{
\footnotesize
\mathclap{
k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}
}
}
\htmlData{class=fragment d-print-none,fragment-index=6}{
\footnotesize
\mathclap{
k_{\kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\norm{x-x'}^2}{2\kappa^2}}
}
}
$$
$\sigma^2$: variance
$\kappa$: length scale
$\nu$: smoothness
$\nu\to\infty$: RBF kernel (Gaussian, Heat, Diffusion)
$\nu = 1/2$
$\nu = 3/2$
$\nu = 5/2$
$\nu = \infty$
Work very well for inputs in $\R^n$,
at least for small $n$.
Geometric Learning
Inputs do not lie in $\R^n$:

Manifolds
e.g. in physics (robotics)

Graphs
e.g. for road networks.
Spaces of graphs
e.g. for drug design
Example Problem
Can we build Matérn GPs for this application?
Molecules as Graphs
Need a GP on some set of graphs.
Let us
Define the RBF Kernel
Define the RBF Kernel
All graphs with 3 nodes.
Define the RBF Kernel
All graphs with 3 nodes.
Distance-based approach:
$ k_{\kappa, \sigma^2}(x,x') \!=\! \sigma^2 \exp \del{\!-\frac{\|x - x'\|^2}{2\kappa^2}} $
$ k_{\kappa, \sigma^2}^{(d)}(x,x') \!=\! \sigma^2 \exp \del{\!-\frac{d(x,x')^2}{2\kappa^2}} $
where $d$ is, e.g., the Hamming distance.
Claim. It is not positive semi-definite.
(this is a very general phenomenon)
Define the RBF Kernel
All graphs with 3 nodes.
All graphs with 3 nodes.
Another characterization of $k_{\kappa, \sigma^2}$:
$k_{\kappa, \sigma^2} \propto \sigma^2 \exp(-\frac{\kappa^2}{2} \Delta)$
where $\Delta$ is the Laplacian on $\R^n$.
Define a different notion of geometry.
Claim. It is always positive definite.
(this is a very general phenomenon)
Compute the RBF Kernel
Naïvely, requires working with $$ \htmlData{class=fragment}{ \Delta \in \R^{2^d \x 2^d}, \htmlData{class=fragment}{ \quad d = n(n-1) / 2, \quad n = \text{ number of nodes.} } } $$
In a smart way: $$ \htmlData{class=fragment}{ \begin{aligned} k_{\kappa, \sigma^2}(x, x') = \sigma^2 \tanh(\kappa^2/2)^{d(x, x')} & \htmlData{class=fragment}{ = \sigma^2 \exp\del{-\frac{d(x, x')}{2 \tilde{\kappa}^2}} } \\ & \htmlData{class=fragment}{ \neq \sigma^2 \exp\del{-\frac{d(x, x')^2}{2 \tilde{\kappa}^2}} } \end{aligned} } $$
Compute the Rest of Matérn Kernels
In a smart way: $$ k_{\nu, \kappa, \sigma^2}(x, x') \propto \sigma^2 \sum_{j=0}^d \del{\frac{2 \nu}{\kappa^2} + 2 j}^{-\nu} G_{j}(d(x, x')), $$ where $G_{j}$ are known orthogonal polynomials (Kravchuk polynomials).
So far we assumed, e.g., $\smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg2.svg}} \not= \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg3.svg}}$.
Often we want $\smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg2.svg}} = \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg3.svg}} = \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg4.svg}}$, etc.
Equivalence Classes of Graphs
Space of equivalence classes for $n=4$
as a quotient graph
Hardness result: kernels are intractable. However, they can be approximated.
Geometric GPs:
other settings
Geometric GPs:
other settings

Simple manifolds:
meshes, spheres, tori
Borovitskiy et al. (AISTATS 2020)

Compact Lie groups and
homogeneous spaces:
$\small\f{SO}(n)$, resp. $\small\f{Gr}(n, r)$
Azangulov et al. (JMLR 2024)
Non-compact symmetric
spaces: $\small\bb{H}_n$ and $\small\f{SPD}(n)$
Azangulov et al. (JMLR 2024)
Geometric GPs: other settings

Vector fields on simple manifolds
Robert-Nicoud et al. (AISTATS 2024)
Geometric GPs: other settings
Edges of graphs
Yang et al. (AISTATS 2024)
Metric graphs
Bolin et al. (Bernoulli 2024)
Cellular Complexes
Alain et al. (ICML 2024)
Spaces of Graphs
Borovitskiy et al. (AISTATS 2023)
Implicit geometry
Semi-supervised learning:
scalar functions
Fichera et al. (NeurIPS 2023)

Semi-supervised learning:
vector fields
Peach et al. (ICLR 2024)
Theoretical results
Theoretical results
Hyperparameter inference
Li et al. (JMLR 2024)
Minimax errors
Rosa et al. (NeurIPS 2023)
More Applications
Robotics: Bayesian optimization of control policies
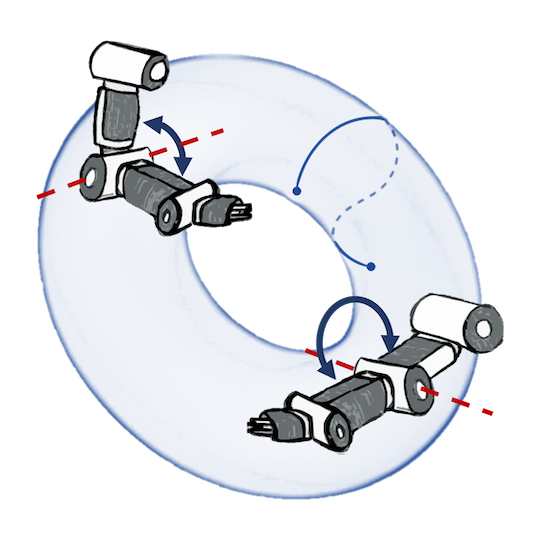
Joint postures: $\mathbb{T}^d$
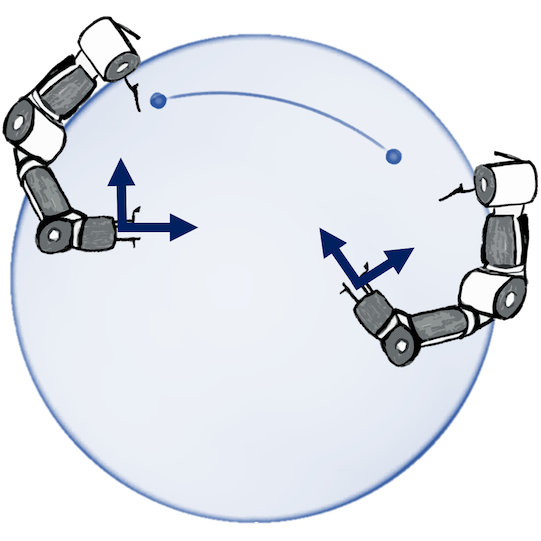
Rotations: $\mathbb{S}_3$, $\operatorname{SO}(3)$
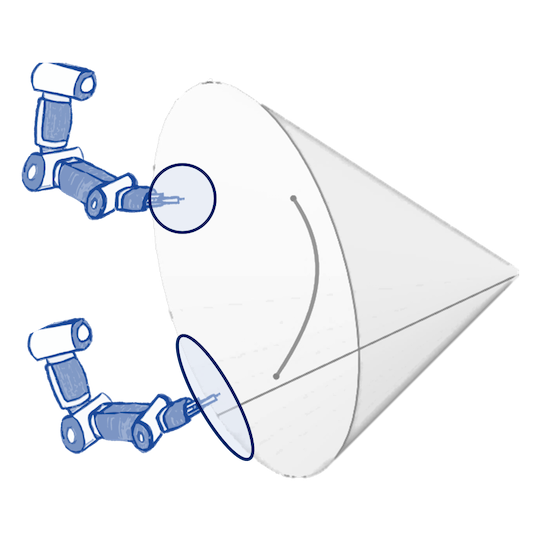
Manipulability: $\operatorname{SPD(3)}$
Medicine: probabilistic atrial activation maps
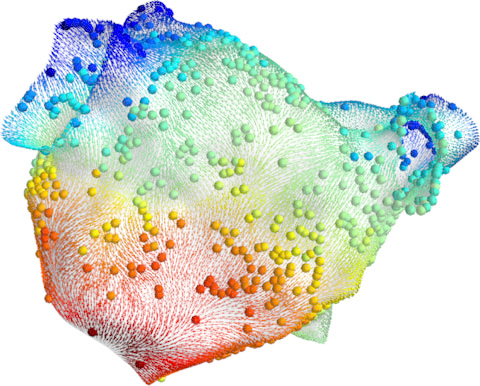
Prediction
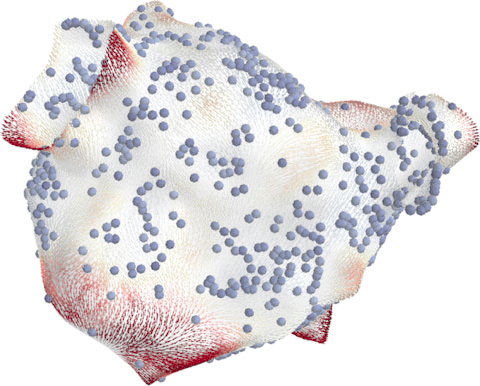
Uncertainty
Matérn Gaussian processes on meshes (independently proposed)
Climate: modeling wind fields

Observations
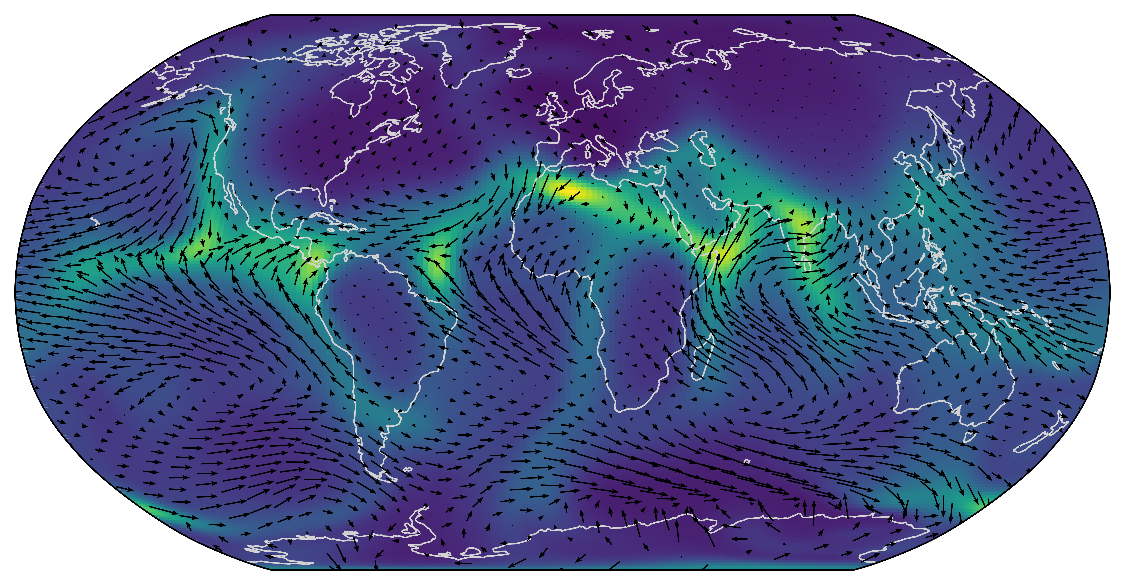
Mean prediction & uncertainty
Software
GeometricKernels: Matérn and heat kernels on geometric domains
https://geometric-kernels.github.io/
Matérn and Heat Kernels on Geometric Domains
Example code:
>>> # Define a space (2-dim sphere).
>>> hypersphere = Hypersphere(dim=2)
>>> # Initialize kernel.
>>> kernel = MaternGeometricKernel(hypersphere)
>>> params = kernel.init_params()
>>> # Compute and print out the 3x3 kernel matrix.
>>> xs = np.array([[0., 0., 1.], [0., 1., 0.], [1., 0., 0.]])
>>> print(kernel.K(params, xs))
[[1. 0.356 0.356]
[0.356 1. 0.356]
[0.356 0.356 1. ]]
Playground: try and compare with baselines
Thank you!
Thank you!
References
References
V. Borovitskiy, I. Azangulov, A. Terenin, P. Mostowsky, M. P. Deisenroth, and N. Durrande. Matérn Gaussian Processes on Graphs. Artificial Intelligence and Statistics, 2021.
A. Feragen, F. Lauze, and S. Hauberg. Geodesic exponential kernels: When curvature and linearity conflict. Computer Vision and Pattern Recognition, 2015.
I. J. Schoenberg. Metric spaces and positive definite functions. Transactions of the American Mathematical Society, 1938.
P. Whittle. Stochastic-processes in several dimensions. Bulletin of the International Statistical Institute, 1963.
F. Lindgren, H. Rue, and J. Lindström. An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. Journal of the Royal Statistical Society, Series B: Statistical Methodology, 2011.
V. Borovitskiy, A. Terenin, P. Mostowsky, and M. P. Deisenroth. Matérn Gaussian Processes on Riemannian Manifolds. Advances in Neural Information Processing Systems, 2020.
I. Azangulov, A. Smolensky, A. Terenin, and V. Borovitskiy. Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces I: the compact case. Journal of Machine Learning Research, 2024.
I. Azangulov, A. Smolensky, A. Terenin, and V. Borovitskiy. Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces II: non-compact symmetric spaces, 2024.
D. Robert-Nicoud, A. Krause, and V. Borovitskiy. Intrinsic Gaussian Vector Fields on Manifolds. Artificial Intelligence and Statistics, 2024.
M. Yang, V. Borovitskiy, and E. Isufi. Hodge-Compositional Edge Gaussian Processes. Artificial Intelligence and Statistics, 2024.
D. Bolin, A. B. Simas, and J. Wallin. Gaussian Whittle-Matérn fields on metric graphs. Bernoulli, 2024.
M. Alain, S. Takao, B. Paige, and M. P. Deisenroth. Gaussian Processes on Cellular Complexes. International Conference on Machine Learning, 2024.
References
V. Borovitskiy, M. R. Karimi, V. R. Somnath, and A. Krause. Isotropic Gaussian Processes on Finite Spaces of Graphs. Artificial Intelligence and Statistics, 2023.
B. Fichera, V. Borovitskiy, A. Krause, and A. Billard. Implicit Manifold Gaussian Process Regression. Advances in Neural Information Processing Systems, 2023.
R. Peach, M. Vinao-Carl, N. Grossman, and M. David. Implicit Gaussian process representation of vector fields over arbitrary latent manifolds. International Conference on Learning Representations, 2024.
D. Li, W. Tang, and S. Banerjee. Inference for Gaussian Processes with Matern Covariogram on Compact Riemannian Manifolds. Journal of Machine Learning Research, 2023.
P. Rosa, V. Borovitskiy, A. Terenin, and J. Rousseau. Posterior Contraction Rates for Matérn Gaussian Processes on Riemannian Manifolds. Advances in Neural Information Processing Systems, 2023.
N. Jaquier, V. Borovitskiy, A. Smolensky, A. Terenin, T. Asfour, and L. Rozo. Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels. Conference on Robot Learning, 2021.
N. Jaquier, L. Rozo, S. Calinon, and M. Bürger. Bayesian optimization meets Riemannian manifolds in robot learning. Conference on Robot Learning, 2020.
S. Coveney, C. Corrado, C. H. Roney, R. D. Wilkinson, J. E. Oakley, F. Lindgren, S. E. Williams, M. D. O'Neill, S. A. Niederer, and R. H. Clayton. Probabilistic interpolation of uncertain local activation times on human atrial manifolds. IEEE Transactions on Biomedical Engineering, 2019.
S. Coveney, C. Corrado, C. H. Roney, D. OHare, S. E. Williams, M. D. O'Neill, S. A. Niederer, R. H. Clayton, J. E. Oakley, and R. D. Wilkinson. Gaussian process manifold interpolation for probabilistic atrial activation maps and uncertain conduction velocity. Philosophical Transactions of the Royal Society A, 2020.