NeurIPS Workshop on Gaussian Processes, Spatiotemporal Modeling, and Decision-making Systems
Geometry-aware
Gaussian Processes
Viacheslav Borovitskiy (Slava)
Consider a simple dynamical system: a pendulum
$$ \htmlData{fragment-index=0,class=fragment}{ x_0 } \qquad \htmlData{fragment-index=1,class=fragment}{ x_1 = x_0 + f(x_0)\Delta t } \qquad \htmlData{fragment-index=2,class=fragment}{ x_2 = x_1 + f(x_1)\Delta t } \qquad \htmlData{fragment-index=3,class=fragment}{ .. } $$
Consider a Simple Dynamical System: a Pendulum
$$ x_0 \qquad x_1 = x_0 + f(x_0)\Delta t \qquad x_2 = x_1 + f(x_1)\Delta t \qquad .. $$
Consider a Simple Dynamical System: a Pendulum
$$f: \R \x \R \to \R \x \R$$
assume $f$ unknown, model $f$ as a GP.
$$ x_0 \qquad x_1 = x_0 + f(x_0)\Delta t \qquad x_2 = x_1 + f(x_1)\Delta t \qquad .. $$
Pendulum Dynamics: Phase Portrait
Pendulum Dynamics: Phase Portrait
Pendulum Dynamics: Phase Portrait
Pendulum Dynamics: Phase Portrait
Phase portrait is periodic!
I.e. the state space is actually a cylinder!
Need priors on non-Euclidean domains!
And they have to be geometry-aware.
Non-Euclidean Domains
Manifolds
e.g. in physics (robotics)
Graphs
e.g. for road networks
Spaces of graphs
e.g. for drug design
Standard Priors
Matérn Gaussian Processes
$$
\htmlData{class=fragment fade-out,fragment-index=6}{
\footnotesize
\mathclap{
k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\abs{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\abs{x-x'}}{\kappa}}
}
}
\htmlData{class=fragment d-print-none,fragment-index=6}{
\footnotesize
\mathclap{
k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\abs{x-x'}^2}{2\kappa^2}}
}
}
$$
$\sigma^2$: variance
$\kappa$: length scale
$\nu$: smoothness
$\nu\to\infty$: RBF kernel (Gaussian, Heat, Diffusion)
$\nu = 1/2$
$\nu = 3/2$
$\nu = 5/2$
$\nu = \infty$
How to generalize these
to non-Euclidean settings?
Distance-based Approach
$$ k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2\exp\del{-\frac{|x - x'|^2}{2\kappa^2}} $$
$$ k_{\infty, \kappa, \sigma^2}^{(d)}(x,x') = \sigma^2\exp\del{-\frac{d(x,x')^2}{2\kappa^2}} $$
For manifolds. Not well-defined unless the manifold is isometric to a Euclidean space.
(Feragen et al. 2015)
For graphs. Not well-defined unless nodes can be isometrically embedded into a Hilbert space.
(Schonberg, 1930s)
For spaces of graphs. What is a space of graphs?!
Need a different generalization
Another Approach: Stochastic Partial Differential Equations
$$ \htmlData{class=fragment,fragment-index=0}{ \underset{\t{Matérn}}{\undergroup{\del{\frac{2\nu}{\kappa^2} - \Delta}^{\frac{\nu}{2}+\frac{d}{4}} f = \c{W}}} } $$ $\Delta$: Laplacian $\c{W}$: Gaussian white noise $d$: dimension
Generalizes well
Geometry-aware: invariant to symmetries of the space
Implicit: no formula for the kernel
Making it explicit:
Continuous case (manifolds)
Solution for Compact Riemannian Manifolds
The solution is a Gaussian process with kernel $$ \htmlData{fragment-index=2,class=fragment}{ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^\infty \del{\frac{2\nu}{\kappa^2} - \lambda_n}^{-\nu-\frac{d}{2}} f_n(x) f_n(x') } $$
$\lambda_n, f_n$: eigenvalues and eigenfunctions of the Laplace–Beltrami operator
How to get $\lambda_n, f_n$?
Answer I: Discretize the Problem
Mesh the manifold, consider the discretized Laplace–Beltrami (a matrix).
Answer II: Use Algebraic Structure
For manifolds with rich group of symmetries, termed homogeneous spaces.
These includes
- Lie groups, like rotations $\mathrm{SO}(n)$ and unitary matrices $\mathrm{SU}(n)$,
- «Proper» homogeneous spaces, e.g. spheres $\mathbb{S}_n$, hyperbolic spaces $\mathbb{H}_n$.
$\lambda_n, f_n$ are connected to representation theory of the group of symmetries.
Riemannian Matérn kernels: Samples
Sphere $\mathbb{S}_2$
Torus $\mathbb{S} \x \mathbb{S}$
Projective plane $\mathrm{RP}^2$
Samples from $\mathrm{GP}(0, k_{\infty})$
Driven by Generalized Random Phase Fourier Features (GRPFF)
Applications: Bayesian Optimization in Robotics
Joint postures: $\mathbb{T}^d$
Rotations: $\mathbb{S}_3$, $\operatorname{SO}(3)$
Manipulability: $\operatorname{SPD(3)}$
Application: Wind Speed Modeling (Vector Fields on Manifolds)
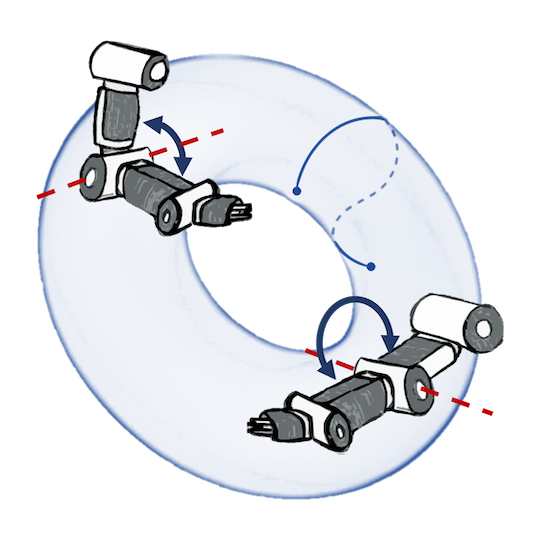
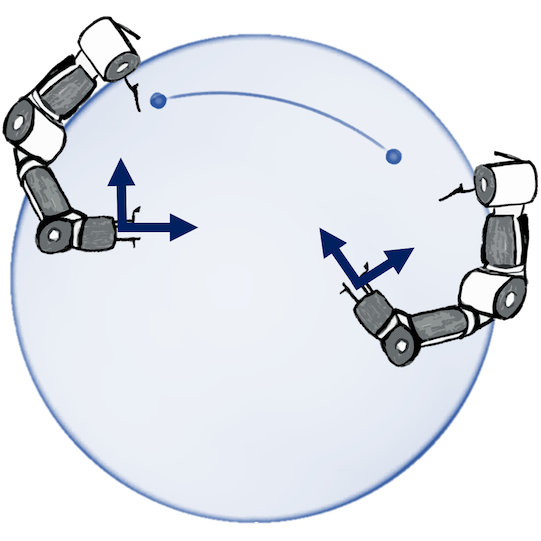
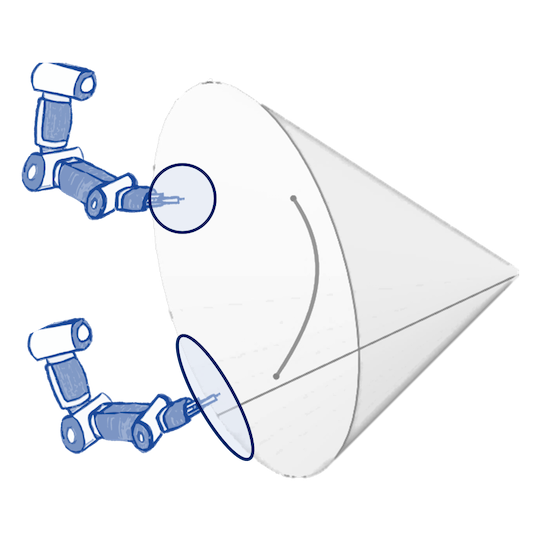
Geometry-aware vs Euclidean
Making it explicit:
Discrete case (graphs)
Matérn Kernels: Finite Undirected Graphs
The solution is a Gaussian process with kernel $$ \htmlData{fragment-index=2,class=fragment}{ k_{\nu, \kappa, \sigma^2}(i, j) = \frac{\sigma^2}{C_{\nu, \kappa}} \sum_{n=0}^{\abs{V}-1} \del{\frac{2\nu}{\kappa^2} + \mathbf{\lambda_n}}^{-\nu} \mathbf{f_n}(i)\mathbf{f_n}(j) } $$
$\lambda_n, \mathbf{f_n}$: eigenvalues and eigenvectors of the Laplacian matrix
Traffic Speed Extrapolation on a Road Network
(a) Prediction
(b) Standard Deviation
Making it explicit:
Discrete case (spaces of graphs)
Spaces of Graphs
Consider the set of all unweighted graphs with $n$ nodes.
It is finite!
How to give it a geometric structure?
Make it into a space?
Graphs define geometry of discrete sets. We make it into a node set of a graph!
Space of graphs with $n = 3$ nodes
as the $3$-dimensional cube
Spaces of Graphs
Beyond functions of actual graphs ($f\big(\smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg2.svg}}\big)$), it is useful to consider equivalence classes of graphs: $f\big(\big\{\smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg2.svg}}, \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg3.svg}}, \smash{\includegraphics[height=2.5em,width=1.0em]{figures/gg4.svg}}\big\}\big)$.
Space of equivalence classes for $n=4$
as the quotient graph of the $4$-d cube
Spaces of Graphs
Space of graphs with $n = 3$ nodes
as the $3$-dimensional cube
Space of equivalence classes for $n=4$
as the quotient graph of the $4$-d cube
Spaces of Graphs
Space of graphs with $n = 3$ nodes
as the $3$-dimensional cube
Space of equivalence classes for $n=4$
as the quotient graph of the $4$-d cube
Application: Drug Design
Conclusion
Implementation
https://geometric-kernels.github.io/
Final Words
For On-site Discussions
Alex Terenin
Thank you!
Thank you!
Slides:
viacheslav.borovitskiy@gmail.com
https://vab.im