Definition. A Gaussian process is random function $f$ on a set $X$ such that for any $x_1,..,x_n \in X$, the vector $f(x_1),..,f(x_n)$ is multivariate Gaussian.

The distribution of a Gaussian process is characterized by

• a mean function $m(x) = \E(f(x))$,
• a kernel (covariance) function $k(x, x') = \Cov(f(x), f(x'))$,

Notation: $f \~ \f{GP}(m, k)$.

The kernel $k$ must be positive (semi-)definite, i.e. for all $x_1, .., x_n \in X$
the matrix $K_{\v{x} \v{x}} := \cbr{k(x_i, x_j)}_{\substack{1 \leq i \leq n \\ 1 \leq j \leq n}}$ must be positive (semi-)definite.

Takes

• a prior Gaussian Process $\f{GP}(m, k)$
• and data $(x_1, y_1), .., (x_n, y_n) \in X \x \R$,

giving the posterior (conditional) Gaussian process $\f{GP}(\hat{m}, \hat{k})$.

The functions $\hat{m}$ and $\hat{k}$ may be explicitly expressed in terms of $m$ and $k$.

Goal: minimize unknown function $\phi$ in as few evaluations as possible.

1. Build GP posterior $f \given \v{y}$ using data $(x_1,\phi(x_1)),..,(x_n,\phi(x_n))$.
2. Choose $$ \htmlClass{fragment}{ x_{n+1} = \argmax_{x\in\c{X}} \underbrace{\alpha_{f\given\v{y}}(x).}_{\text{acquisition function}} } $$ For instance, expected improvement $$ \alpha_{f\given\v{y}}(x) = \E_{f\given\v{y}} \max(0, {\displaystyle\min_{i=1,..,n}} \phi(x_i) - f(x)). $$

Also

• geostatistics,
• robotics,
• more...

$$ \htmlData{class=fragment fade-out,fragment-index=9}{ \footnotesize \mathclap{ k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}} } } \htmlData{class=fragment d-print-none,fragment-index=9}{ \footnotesize \mathclap{ k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\norm{x-x'}^2}{2\kappa^2}} } } $$ $\sigma^2$: variance $\kappa$: length scale $\nu$: smoothness
$\nu\to\infty$: Gaussian kernel (Heat, Diffusion, RBF)

$\nu = 1/2$

$\nu = 3/2$

$\nu = 5/2$

$\nu = \infty$

Manifolds

Graphs

How should Matérn kernels generalize to this setting?

$$ k_{\infty, \kappa, \sigma^2}^{(d_g)}(x,x') = \sigma^2\exp\del{-\frac{d_g(x,x')^2}{2\kappa^2}} $$

Theorem. (Feragen et al.) Let $M$ be a complete Riemannian manifold without boundary. If $k_{\infty, \kappa, \sigma^2}^{(d_g)}$ is positive semi-definite for all $\kappa$, then $M$ is isometric to a Euclidean space.

For Matérn kernels: apparently an open problem.

Need a different candidate generalization

$$ \htmlData{class=fragment,fragment-index=0}{ \underset{\t{Matérn}}{\undergroup{\del{\frac{2\nu}{\kappa^2} - \Delta}^{\frac{\nu}{2}+\frac{d}{4}} f = \c{W}}} } $$ $\Delta$: Laplacian $\c{W}$: Gaussian white noise

The solution is a Gaussian process with kernel $$ \htmlData{fragment-index=2,class=fragment}{ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_\nu} \sum_{n=0}^\infty \del{\frac{2\nu}{\kappa^2} - \lambda_n}^{-\nu-\frac{d}{2}} f_n(x) f_n(x') } $$

$\lambda_n, f_n$: eigenvalues and eigenfunctions of the Laplace–Beltrami operator

Mesh the manifold, consider the discretized Laplace–Beltrami (a matrix).

Manifold: Lie group. Metric: Killing form. Laplacian ≡ Casimir.

Eigenfunctions ≡ matrix coefficients of unitary irreducible representations.

$$ \begin{aligned} \htmlData{class=fragment}{k(x,y)} &\htmlData{class=fragment}{= \frac{\sigma^2}{C_\nu} \sum_{n=0}^\infty \del{\frac{2\nu}{\kappa^2} - \lambda_n}^{-\nu-\frac{d}{2}} f_n(x) f_n(y) } \\ &\htmlData{class=fragment}{= \frac{\sigma^2}{C_{\nu}}\sum_{\pi} \del{\frac{2\nu}{\kappa^2} - \lambda_{\pi}}^{-\nu-\frac{d}{2}} d_{\pi} \chi_{\pi}(y^{-1} x). } \end{aligned} $$

Compute $\chi_{\pi}$: Weyl character formula. Compute $\lambda_{\pi}$: Freudenthal’s formula.

Manifold: Hogenous space $G/H$. Metric: Inherited from the Lie group $G$.

Eigenfunctions ≡ spherical functions (for $G/H = \mathbb{S}_d$—spherical harmonics).

Characters $\chi_{\pi}$ are changed to zonal spherical functions $\phi_{\pi}$. For $G/H = \mathbb{S}_d$ — zonal spherical harmonics (certain Gegenbauer polynomials of distance).

Eigenvalues — same as for $G$.

$$ \begin{aligned} k(x,y) = \frac{\sigma^2}{C_{\nu}}\sum_{\pi} \del{\frac{2\nu}{\kappa^2} - \lambda_{\pi}}^{-\nu-\frac{d}{2}} d_{\pi} \phi_{\pi}(y^{-1} x). \end{aligned} $$

$k_{1/2}(\htmlStyle{color:rgb(255, 19, 0)!important}{\bullet},\.)$

The solution is a Gaussian process with kernel $$ \htmlData{fragment-index=2,class=fragment}{ k_{\nu, \kappa, \sigma^2}(i, j) = \frac{\sigma^2}{C_{\nu}} \sum_{n=0}^{\abs{V}-1} \del{\frac{2\nu}{\kappa^2} + \mathbf{\lambda_n}}^{-\nu} \mathbf{f_n}(i)\mathbf{f_n}(j) } $$

$\lambda_n, \mathbf{f_n}$: eigenvalues and eigenvectors of the Laplacian matrix

$k_{5/2}(\htmlStyle{color:rgb(255, 19, 0)!important}{\circ},\.)$

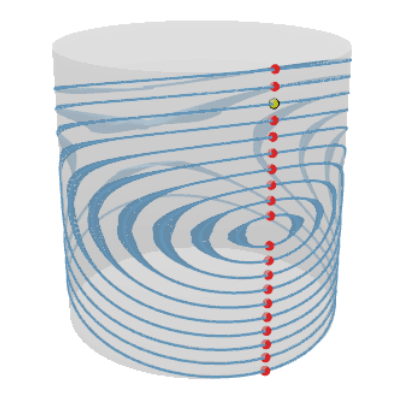
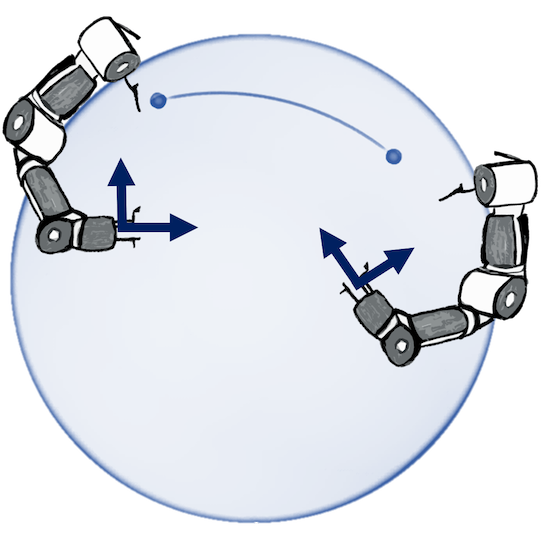
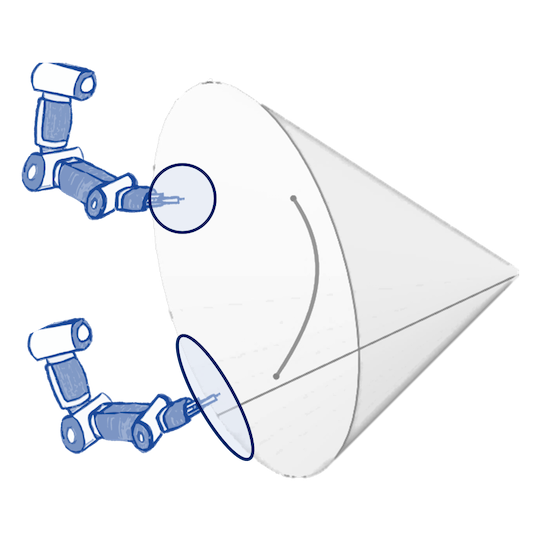
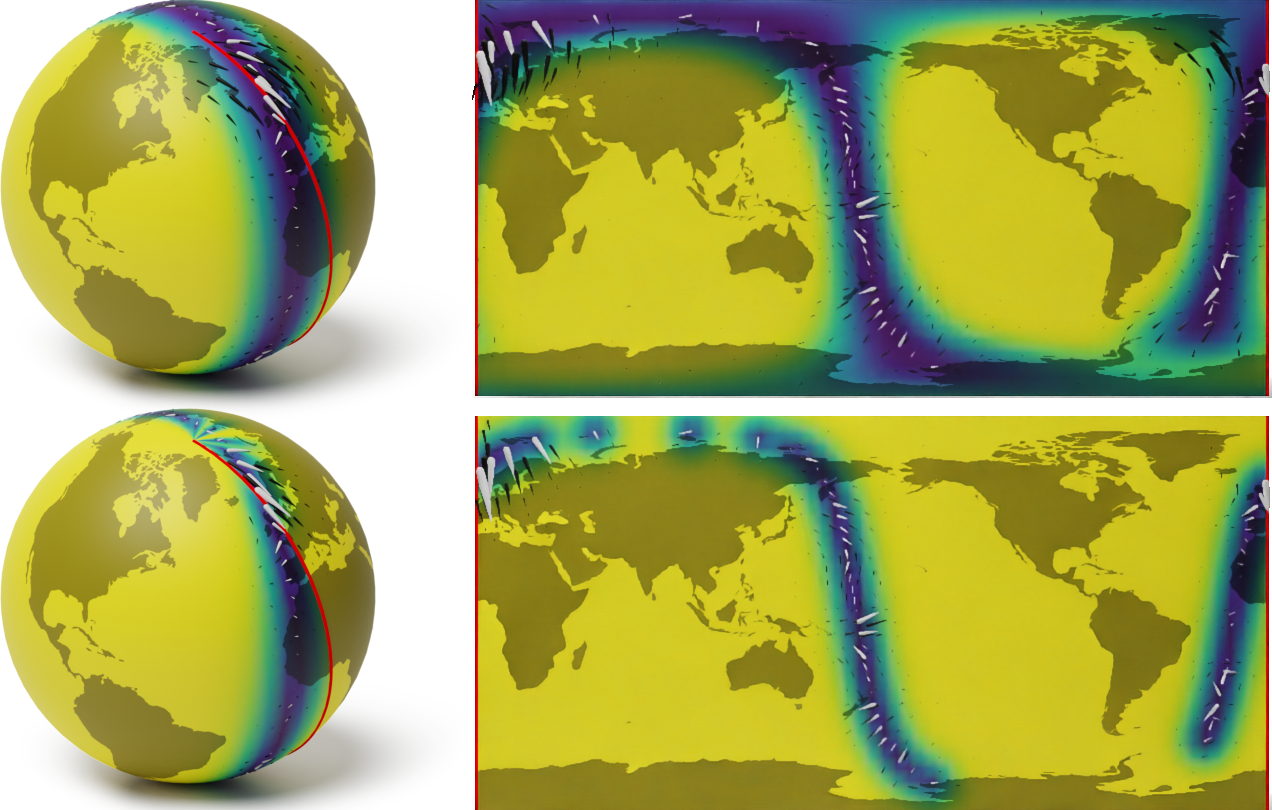
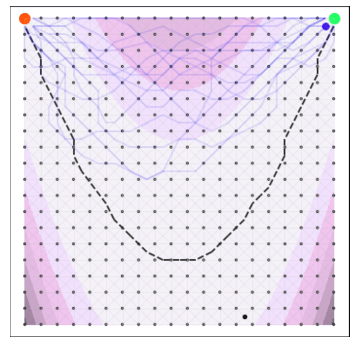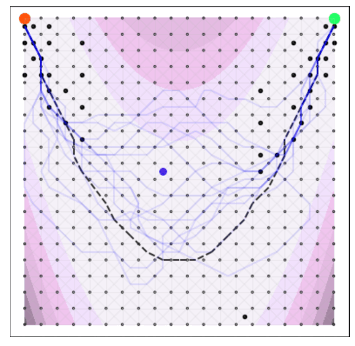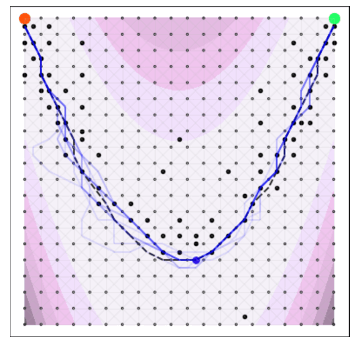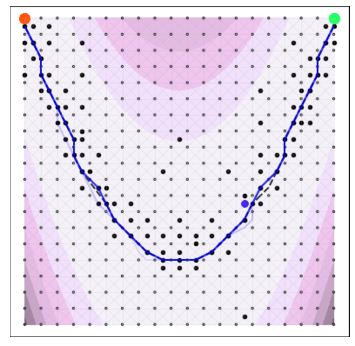
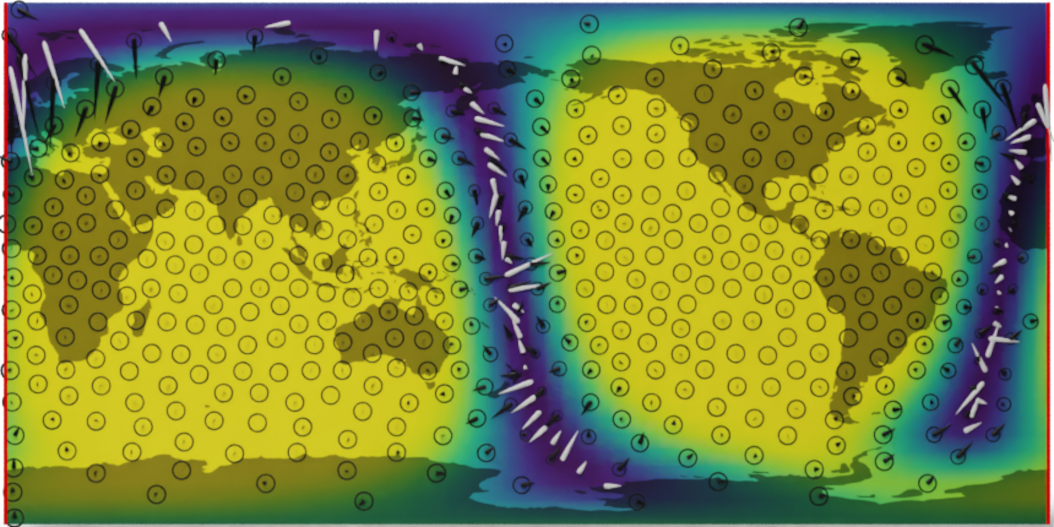
A naive Euclidean model

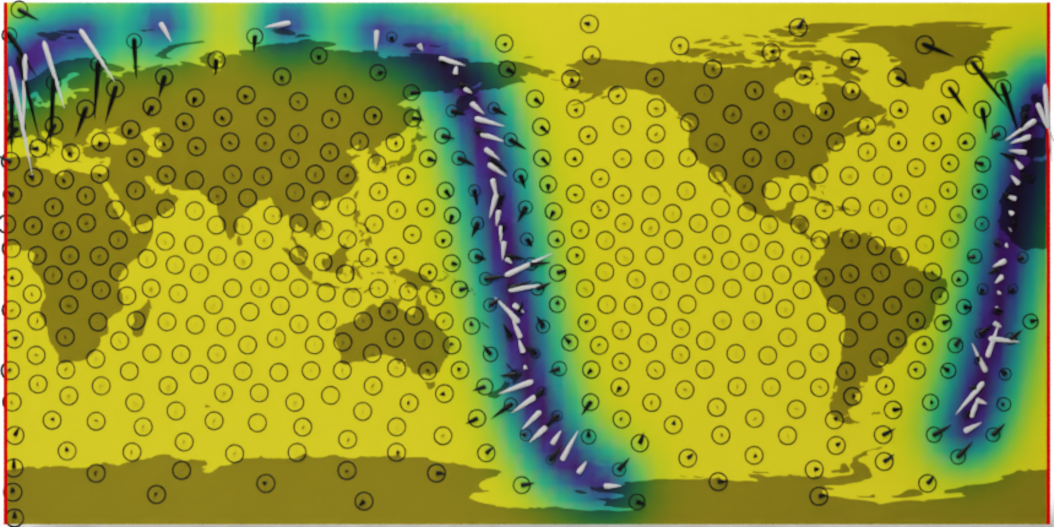
Wind speed extrapolation on a map

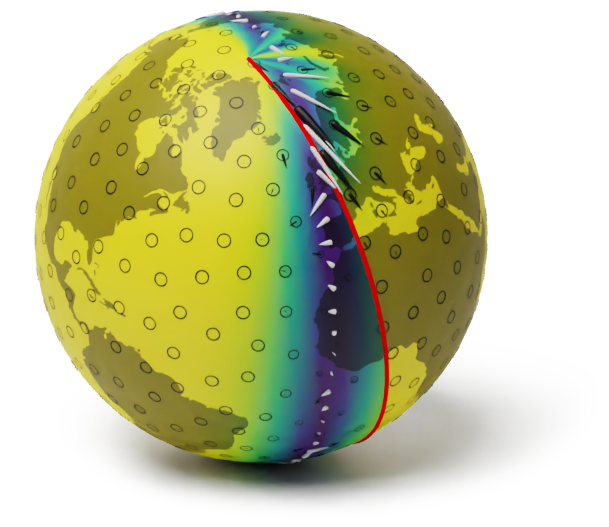
The corresponding model on a globe

A geometry-aware model

Wind speed extrapolation on a map

The corresponding model on a globe

References

V. Borovitskiy, A. Terenin, P. Mostowsky, M. P. Deisenroth. Matérn Gaussian Processes on Riemannian Manifolds.
In Neural Information Processing Systems (NeurIPS) 2020.

V. Borovitskiy, I. Azangulov, A. Terenin, P. Mostowsky, M. P. Deisenroth. Matérn Gaussian Processes on Graphs.
In International Conference on Artificial Intelligence and Statistics (AISTATS) 2021.

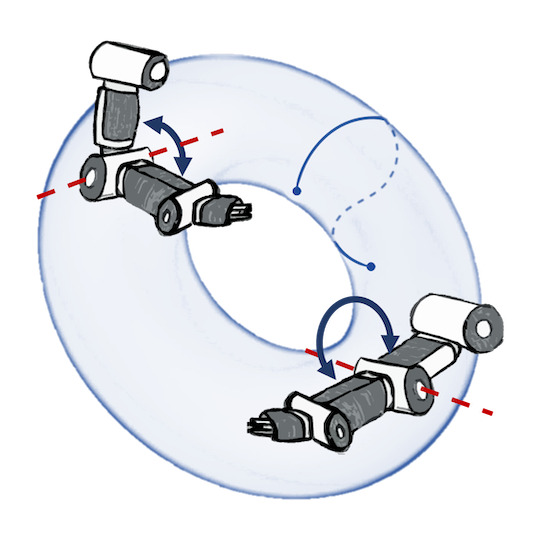
N. Jaquier, V. Borovitskiy, A. Smolensky, A. Terenin, T. Asfour and L. Rozo. Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels. In Conference on Robot Learning (CoRL) 2021.

I. Azangulov, A. Smolensky, A. Terenin, V. Borovitskiy. Stationary Kernels and Gaussian Processes on Lie Groups and their Homogeneous Spaces I: the Compact Case. Preprint arXiv:2208.14960, 2022.

P. Whittle. On Stationary Processes in the Plane. In Biometrika, 1954.

F. Lindgren, H. Rue, J. Lindström. An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. In Journal of the Royal Statistical Society: Series B, 2011.

A. Feragen, F. Lauze, S. Hauberg. Geodesic exponential kernels: When curvature and linearity conflict. In IEEE conference on computer vision and pattern recognition (CVPR) 2015.

M. Deisenroth, C. E. Rasmussen. PILCO: A model-based and data-efficient approach to policy search. In International Conference on machine learning (ICML) 2011.

W. Neiswanger, K. A. Wang, S. Ermon. Bayesian algorithm execution: Estimating computable properties of black-box functions using mutual information. In International Conference on Machine Learning (ICML) 2021.