Sequential Decision Making
Gaussian processes — gold standard in uncertainty estimation
Gaussian Processes
Definition. A Gaussian process is random function $f : X \times \Omega \to \R$ such that for any $x_1,..,x_n$, the vector $f(x_1),..,f(x_n)$ is multivariate Gaussian.
The distribution of a Gaussian process is characterized by
- a mean function $m(x) = \E(f(x))$,
- a kernel (covariance) function $k(x, x') = \Cov(f(x), f(x'))$,
Notation: $f \~ \f{GP}(m, k)$.
The kernel $k$ must be positive (semi-)definite.
Gaussian Process Regression
Takes
- a prior Gaussian Process $\f{GP}(m, k)$
- and data $(x_1, y_1), .., (x_n, y_n) \in X \x \R$,
giving the posterior Gaussian process $\f{GP}(\hat{m}, \hat{k})$.
The functions $\hat{m}$ and $\hat{k}$ may be explicitly expressed in terms of $m$ and $k$.
An Application: Bayesian Optimization
Goal: minimize unknown function $\phi$ in as few evaluations as possible.
- Build GP posterior $f \given \v{y}$ using data $(x_1,\phi(x_1)),..,(x_n,\phi(x_n))$.
- Choose $$ \htmlClass{fragment}{ x_{n+1} = \argmax_{x\in\c{X}} \underbrace{\alpha_{f\given\v{y}}(x).}_{\text{acquisition function}} } $$ For instance, expected improvement $$ \alpha_{f\given\v{y}}(x) = \E_{f\given\v{y}} \max(0, {\displaystyle\min_{i=1,..,n}} \phi(x_i) - f(x)). $$
Bayesian Optimization 1/15
Bayesian Optimization 2/15
Bayesian Optimization 3/15
Bayesian Optimization 4/15
Bayesian Optimization 5/15
Bayesian Optimization 6/15
Bayesian Optimization 7/15
Bayesian Optimization 8/15
Bayesian Optimization 9/15
Bayesian Optimization 10/15
Bayesian Optimization 11/15
Bayesian Optimization 12/15
Bayesian Optimization 13/15
Bayesian Optimization 14/15
Bayesian Optimization 15/15
Bayesian Optimization
Applications

Also
- geostatistics,
- robotics,
- more...
Efficient Algorithms
Algorithms Connected to Gaussian Processes
Efficient Conditioning
Idea. Approximate the posterior process $\f{GP}(\hat{m}, \hat{k})$ with a simpler process belonging to some parametric family $\f{GP}(m_{\theta}, k_{\theta})$.
$O(N^3)$ turns into $O(N K^2)$ where $K$ controls accuracyEfficient Sampling From Priors
Priors are usually assumed stationary.
Idea. Approximate with a process of form
$$ \htmlData{class=yoyo}{ \tilde{f}(x) = \sum_{l=1}^L w_l \phi_l(x) \qquad w_l \overset{\textrm{i.i.d.}}{\sim} N(0, 1), } $$
which is easy to sample from.
$O(M^3)$ turns into $O(M L)$ where $L$ controls accuracyEfficient Sampling From Posteriors
Idea. From a parametric family $\f{GP}(m_{\theta}, k_{\theta})$ build another family $\f{GP}(\tilde{m}_{\theta}, \tilde{k}_{\theta})$ which is easy to sample from.
$O(N^3 + M^3)$ turns into $O(N K^2 + M L)$ where $K$ and $L$ control accuracyGeometry-aware Priors
on Manifolds and Graphs
Euclidean Priors: Matérn Gaussian Processes
$$
\htmlData{class=fragment fade-out,fragment-index=9}{
\footnotesize
\mathclap{
k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}
}
}
\htmlData{class=fragment d-print-none,fragment-index=9}{
\footnotesize
\mathclap{
k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\norm{x-x'}^2}{2\kappa^2}}
}
}
$$
$\sigma^2$: variance
$\kappa$: length scale
$\nu$: smoothness
$\nu\to\infty$: Gaussian kernel (RBF)
$\nu = 1/2$
$\nu = 3/2$
$\nu = 5/2$
$\nu = \infty$
Gaussian Processes on
Non-Euclidean Domains
Non-Euclidean Domains

Manifolds

Graphs
How should Matérn kernels generalize to this setting?
Explicit Formula for Compact Riemannian Manifolds
$$ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_\nu} \sum_{n=0}^\infty \del{\frac{2\nu}{\kappa^2} - \lambda_n}^{-\nu-\frac{d}{2}} f_n(x) f_n(x') $$
$\lambda_n, f_n$: eigenvalues and eigenfunctions of the Laplace–Beltrami
Examples:


Explicit Formula for Finite Undirected Graphs
$$ k_{\nu, \kappa, \sigma^2}(i, j) = \frac{\sigma^2}{C_{\nu}} \sum_{n=0}^{\abs{V}-1} \del{\frac{2\nu}{\kappa^2} + \mathbf{\lambda_n}}^{-\nu} \mathbf{f_n}(i)\mathbf{f_n}(j) $$
$\lambda_n, \mathbf{f_n}$: eigenvalues and eigenvectors of the Laplacian matrix
Examples:
Graph Matérn kernels: examples
$k_{5/2}(\htmlStyle{color:rgb(255, 19, 0)!important}{\circ},\.)$
An Application: Modeling Dynamical Systems with Uncertainty
$$ \htmlData{fragment-index=0,class=fragment}{ x_0 } \qquad \htmlData{fragment-index=1,class=fragment}{ x_1 = x_0 + f(x_0)\Delta t } \qquad \htmlData{fragment-index=2,class=fragment}{ x_2 = x_1 + f(x_1)\Delta t } \qquad \htmlData{fragment-index=3,class=fragment}{ .. } $$
Pendulum Dynamics: GP on a cylinder

(a) Ground truth
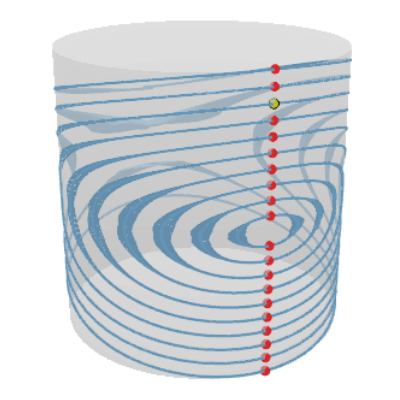
(b) Gaussian process
Traffic Speed Extrapolation on a Road Network
(a) Prediction
(b) Standard Deviation
Wind Speed Modeling: Vector Fields on Manifolds
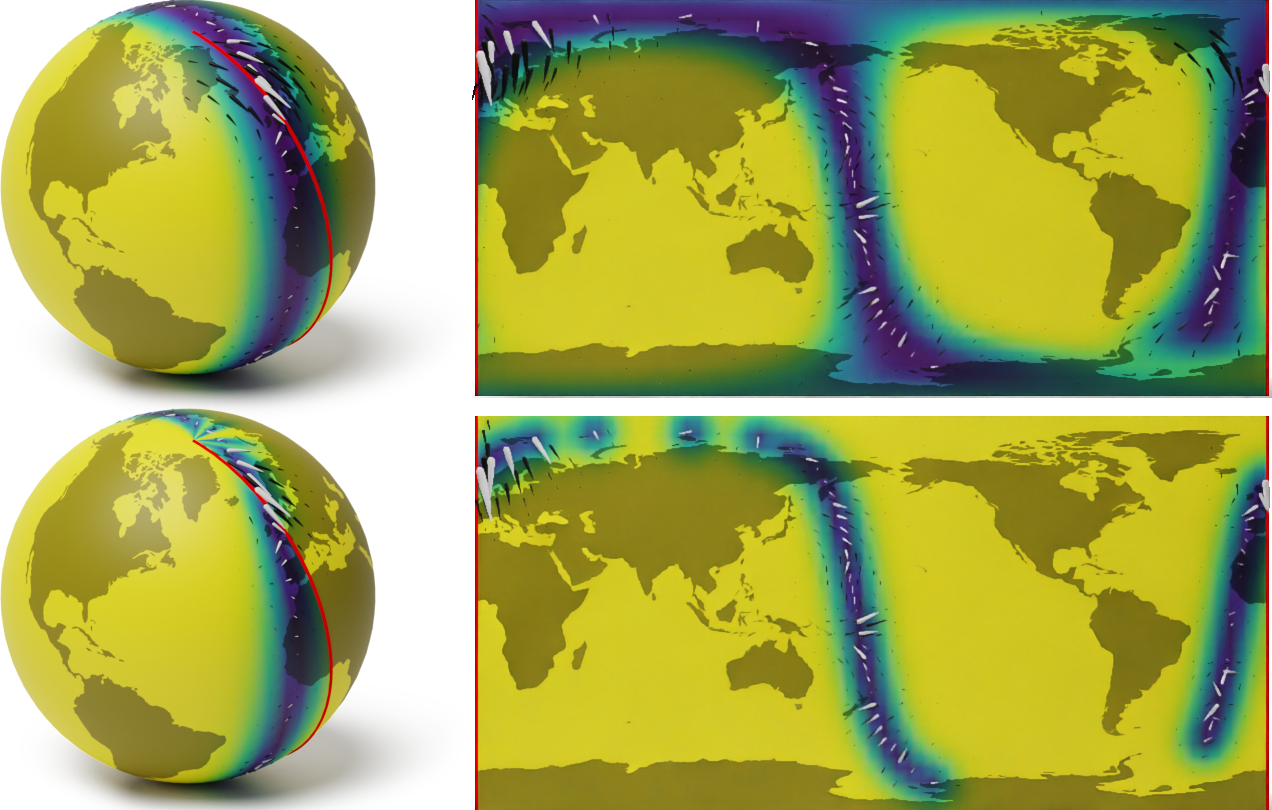
Thank you!
Thank you!
Special thanks: Ekaterina Noskova for the wonderful Bayesian optimization animations. viacheslav.borovitskiy@gmail.com https://vab.imReferences
J. Wilson, V. Borovitskiy, A. Terenin, P. Mostowsky, M. P. Deisenroth. Efficiently sampling functions from Gaussian process posteriors. International Conference on Machine Learning, 2020.
V. Borovitskiy, A. Terenin, P. Mostowsky, M. P. Deisenroth. Matérn Gaussian Processes on Riemannian Manifolds.
In Neural Information Processing Systems (NeurIPS) 2020.
V. Borovitskiy, I. Azangulov, A. Terenin, P. Mostowsky, M. P. Deisenroth. Matérn Gaussian Processes on Graphs.
In International Conference on Artificial Intelligence and Statistics (AISTATS) 2021.
J. Wilson, V. Borovitskiy, A. Terenin, P. Mostowsky, M. P. Deisenroth. Pathwise Conditioning of Gaussian Processes. Journal of Machine Learning Research, 2021.
N. Jaquier, V. Borovitskiy, A. Smolensky, A. Terenin, T. Asfour, L. Rozo. Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels. To appear in Conference on Robot Learning (CoRL), 2021.
M. Hutchinson, A. Terenin, V. Borovitskiy, S. Takao, Y. W. Teh, M. P. Deisenroth. Vector-valued Gaussian Processes on Riemannian Manifolds via Gauge-Independent Projected Kernels. To appear in NeurIPS 2021.
viacheslav.borovitskiy@gmail.com https://vab.im