Конференция SAMPLE
Регрессия на основе
гауссовских процессов
на неевклидовых пространствах
Вячеслав Боровицкий


Определение. Гауссовский процесс это семейство $\cbr{f(x)}_{x \in X}$, где любой конечный набор $f(x_1), .., f(x_n)$ — совместно гауссовский.
Распределение гауссовского процесса определяется
Поэтому пишут $f \~ \f{GP}(m, k)$.
$k$ должна быть положительно определенной, т.е. для $x_1, .., x_n \in X$ матрица $K_{\v{x} \v{x}} := \cbr{k(x_i, x_j)}_{\substack{1 \leq i \leq n \\ 1 \leq j \leq n}}$ положительно определена.
Регрессия на основе гауссовских процессов совмещает
давая условный (апостериорный) гауссовский процесс $\f{GP}(\hat{m}, \hat{k})$.
Функции $\hat{m}$ и $\hat{k}$ явно выражаются через $m$ и $k$.

Еще
$$
\htmlData{class=fragment fade-out,fragment-index=9}{
\footnotesize
\mathclap{
k_{\nu, \kappa, \sigma^2}(x,x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)} \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}^\nu K_\nu \del{\sqrt{2\nu} \frac{\norm{x-x'}}{\kappa}}
}
}
\htmlData{class=fragment d-print-none,fragment-index=9}{
\footnotesize
\mathclap{
k_{\infty, \kappa, \sigma^2}(x,x') = \sigma^2 \exp\del{-\frac{\norm{x-x'}^2}{2\kappa^2}}
}
}
$$
$\sigma^2$: дисперсия
$\kappa$: масштаб
$\nu$: гладкость
$\nu\to\infty$: дает гауссовское ядро
$\nu = 1/2$
$\nu = 3/2$
$\nu = 5/2$
$\nu = \infty$


$$ k_{\infty, \kappa, \sigma^2}^{(d_g)}(x,x') = \sigma^2\exp\del{-\frac{d_g(x,x')^2}{2\kappa^2}} $$
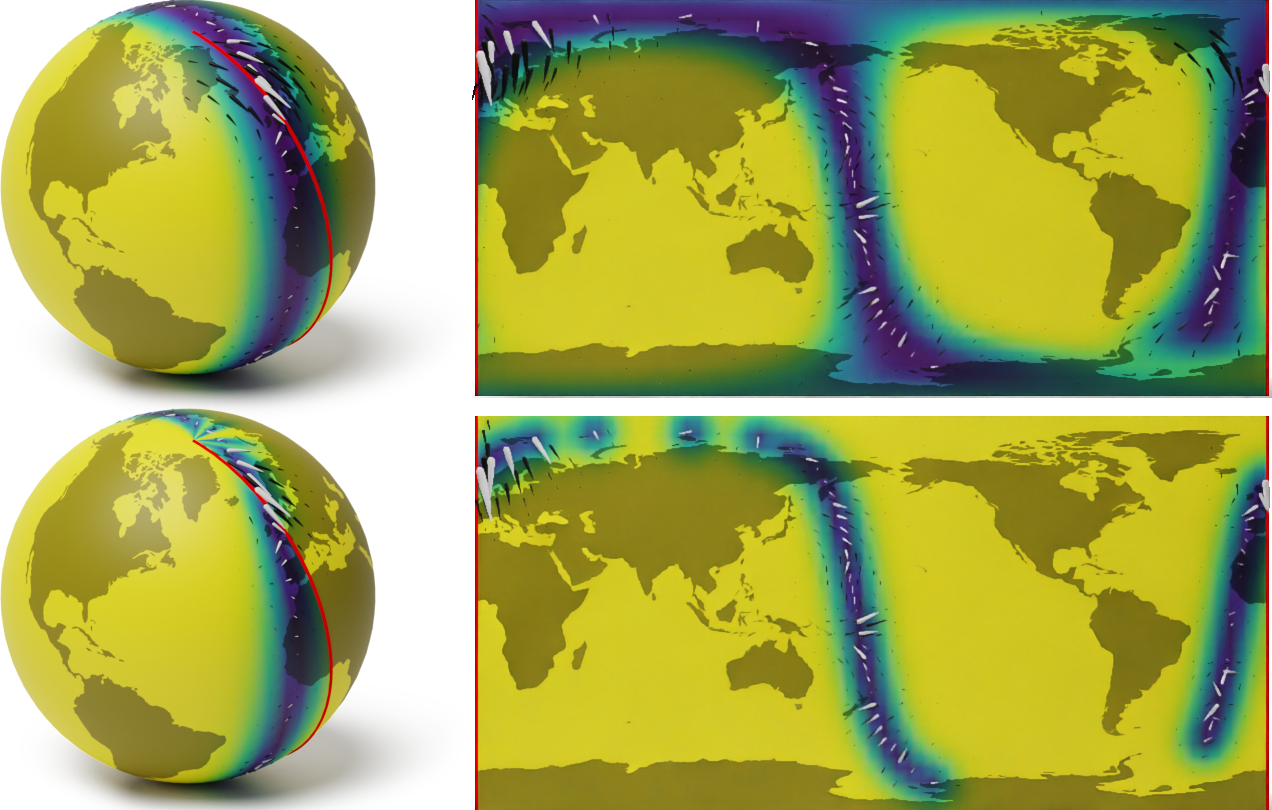
Теорема. (Feragen et al.) Пусть $M$ полное риманово многообразие без края. Если функция $k_{\infty, \kappa, \sigma^2}^{(d_g)}$ положительно определена для всех $\kappa$, то $M$ изометрично Евклидову пространству.
$$ \htmlData{class=fragment,fragment-index=0}{ \underset{\t{Ядро Матерна}}{\undergroup{\del{\frac{2\nu}{\kappa^2} - \Delta}^{\frac{\nu}{2}+\frac{d}{4}} f = \c{W}}} } \qquad \htmlData{class=fragment,fragment-index=1}{ \underset{\t{Гауссово ядро}}{\undergroup{\vphantom{\del{\frac{2\nu}{\kappa^2} - \Delta}^{\frac{\nu}{2}+\frac{d}{4}}} e^{-\frac{\kappa^2}{4}\Delta} f = \c{W}}} } $$ $\Delta$: лапласиан $\c{W}$: белый шум
$$ \htmlData{class=fragment,fragment-index=0}{ \del{\frac{2\nu}{\kappa^2} - \Delta}^{\frac{\nu}{2}+\frac{d}{4}} f = \c{W} } $$
| Компактные многообразия | Графы |
|---|---|
| • $\Delta$ — Лаплас–Бельтрами, | • $\Delta$ — матрица Кирхгофа, |
| • $\c{W}$ — белый шум, порожденный римановым объемом, | • $\c{W}$ — вектор независимых стандартных гауссиан, |
|
• $\left( \frac{2 \nu}{\kappa^2} - \Delta \right)^{\frac{\nu}{2} + \frac{d}{4}}$ определяется через функциональное исчисление |
|
Решением уравнения является гауссовский процесс с ядром $$ \htmlData{class=fragment}{ k_{\nu, \kappa, \sigma^2}(x,x') = \frac{\sigma^2}{C_\nu} \sum_{n=0}^\infty \del{\frac{2\nu}{\kappa^2} - \lambda_n}^{-\nu-\frac{d}{2}} f_n(x) f_n(x') } $$


Решением уравнения является гауссовский процесс с ядром $$ \htmlData{class=fragment}{ k_{\nu, \kappa, \sigma^2}(i, j) = \frac{\sigma^2}{C_{\nu}} \sum_{n=0}^{\abs{V}-1} \del{\frac{2\nu}{\kappa^2} + \mathbf{\lambda_n}}^{-\nu} \mathbf{f_n}(i)\mathbf{f_n}(j) } $$


$$ \htmlData{fragment-index=0,class=fragment}{ x_0 } \qquad \htmlData{fragment-index=1,class=fragment}{ x_1 = x_0 + f(x_0)\Delta t } \qquad \htmlData{fragment-index=2,class=fragment}{ x_2 = x_1 + f(x_1)\Delta t } \qquad \htmlData{fragment-index=3,class=fragment}{ .. } $$












V. Borovitskiy, A. Terenin, P. Mostowsky, M. P. Deisenroth. Matérn Gaussian Processes on Riemannian Manifolds.
In Neural Information Processing Systems (NeurIPS) 2020.
V. Borovitskiy, I. Azangulov, A. Terenin, P. Mostowsky, M. P. Deisenroth. Matérn Gaussian Processes on Graphs.
In International Conference on Artificial Intelligence and Statistics (AISTATS) 2021.
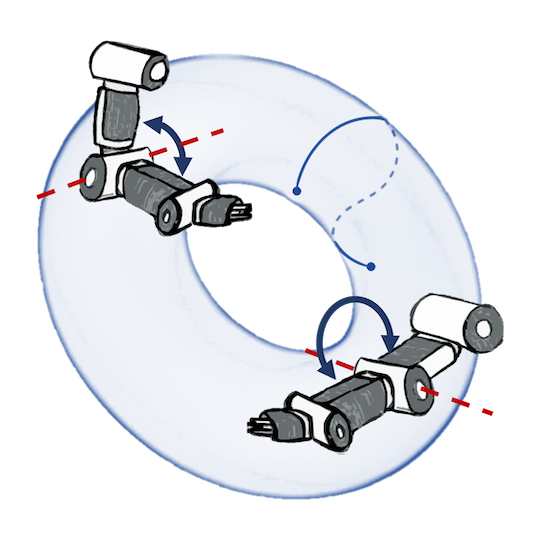
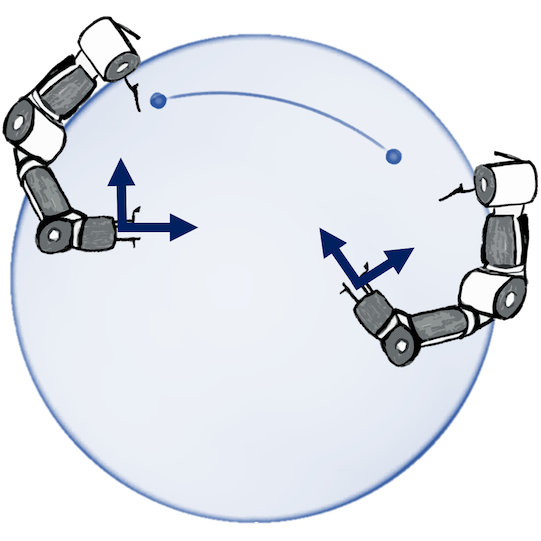
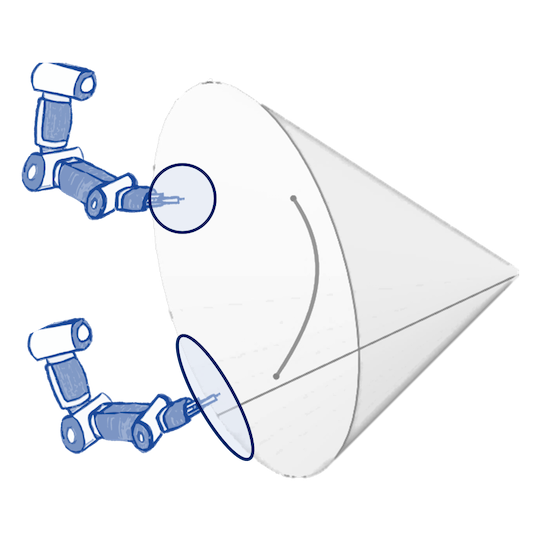
N. Jaquier, V. Borovitskiy, A. Smolensky, A. Terenin, T. Asfour, L. Rozo. Geometry-aware Bayesian Optimization in Robotics using Riemannian Matérn Kernels. To appear in Conference on Robot Learning (CoRL), 2021.
M. Hutchinson, A. Terenin, V. Borovitskiy, S. Takao, Y. W. Teh, M. P. Deisenroth. Vector-valued Gaussian Processes on Riemannian Manifolds via Gauge-Equivariant Projected Kernels. To appear in NeurIPS 2021.
viacheslav.borovitskiy@gmail.com https://vab.im